Самая быстрорастущая функция: Является ли занятой бобр самой быстрорастущей функцией, известной человеку?
Занимательная Гугология, часть 4. Какое число самое большое? (1): scorcher_7 — LiveJournal
Дисклеймер: Перед тем как читать эту статью обязательно прочтите первую, вторую и третью часть этого цикла, иначе вы можете не понять о чем идет речь. К тому же если уже после третьей части у вас голова идет кругом от всех этих математических выражений и знаков, то предупреждаю: здесь их будет еще больше. Но если вы внимательно ознакомились с предыдущими статьями цикла, то это не должно стать для вас барьером.Итак, что мы с вами знаем о больших числах. Во-первых, любое по-настоящему большое число является формализацией, то есть некой условной записью. Представить это число в его естественном количественном виде непосильная задача для человеческого мозга. Во-вторых, мы знаем, что существуют нотации для создания чисел, то есть это некие условные записи цифр и знаков, которые дают нам возможность выразить числа. С математической точки зрения нотации представляют собой функции, в которые мы подставляем меньшие числа (цифры), чтобы получить бо́льшие числа. Чем больше в результате получается число, тем сильнее считается нотация. Но что лежит в основе силы нотаций, то есть функций, которыми они по сути являются? Ответ: чаще всего это рекурсии, реже другие методы. Так или иначе, при создании самого большого числа, все сводится к созданию самой быстрорастущей функции. То есть основным критерием таких функций будет следующее правило: подставляя меньшие аргументы (значения, которые функция принимает) мы получаем все бо́льшие результаты.
Поэтому давайте и мы с вами определим границы для записи самого большого числа, которое позволяет сделать нотация или функция. Договоримся о следующем: запись не должна превышать по содержанию 20 символов. Тогда максимальное число в десятичной нотации будет равно 99 999 999 999 999 999 999 (девяносто девять секстиллионов девятьсот девяносто девять квинтиллионов девятьсот девяносто девять квадриллионов девятьсот девяносто девять триллионов девятьсот девяносто девять миллиардов девятьсот девяносто девять миллионов девятьсот девяносто девять тысяч девятьсот девяносто девять). Одноэтажная логарифмическая закончится на 10999 999 999 999 999 999, что больше чем гугол, но даже близко не дотягивает до гуголплекса. За логарифмической записью идет гипероператорная, которая позволяет создавать вообще уже невообразимые числа, но записать число Грэма в 20 символах и ей не по зубам. Для этого в первой части я создал свою функцию: superhyper(3,3,6,64) — и уложился в аккурат в 20 символов. В общем, я думаю, принцип понятен.
Одноэтажная логарифмическая закончится на 10999 999 999 999 999 999, что больше чем гугол, но даже близко не дотягивает до гуголплекса. За логарифмической записью идет гипероператорная, которая позволяет создавать вообще уже невообразимые числа, но записать число Грэма в 20 символах и ей не по зубам. Для этого в первой части я создал свою функцию: superhyper(3,3,6,64) — и уложился в аккурат в 20 символов. В общем, я думаю, принцип понятен.
Итак, поехали разбираться какая функция или нотация самая сильная и позволит нам записать самое большое число в 20 символах. Но чтобы сравнивать между собой силу нотаций и функций, нам нужен некий универсальный стандарт для сравнения с ним. Хорошо что такой измерительный эталон существует.
В математике есть семейство функций, которые называют функциями быстрорастущей иерархии. Вот их обычно и используют, чтобы сопоставлять с другими быстрорастущими функциями и измерять скорость, с которой они растут. Поэтому если мы хотим добраться до самых больших придуманных чисел, нам нужно понять что же это за функции быстрорастущей иерархии.
Первая в семействе это f0(n), по сути это просто итерация n+1, или проще говоря обычный счет:
f0(5) = 6
f0(10) = 11
Функция банального сложения n+m растет немного быстрее ее, потому как мы можем подставить любое число m, а не только 1.
Теперь внимание! Функция дублирования 2⋅n, считается еще более быстрорастущей, чем сложение. Это очень важно понимать! В случае сложения n+m мы зависим от двух переменных и чтобы увеличить результат нам нужно увеличить оба слагаемых, в случае дублирования же участвует всего одна переменная n+n=2⋅n, а значит для увеличения результата требуется меньше изменений внутри функции. Сформулируем это правило: среди двух почти одинаково растущих функций более быстрорастущей считается та, которая использует меньше аругментов.
Вернемся к функциям быстрорастущей иерархии. Следующей в семействе будет функция f1(n), она определяется рекурсивно от предыдущей функции f0(n).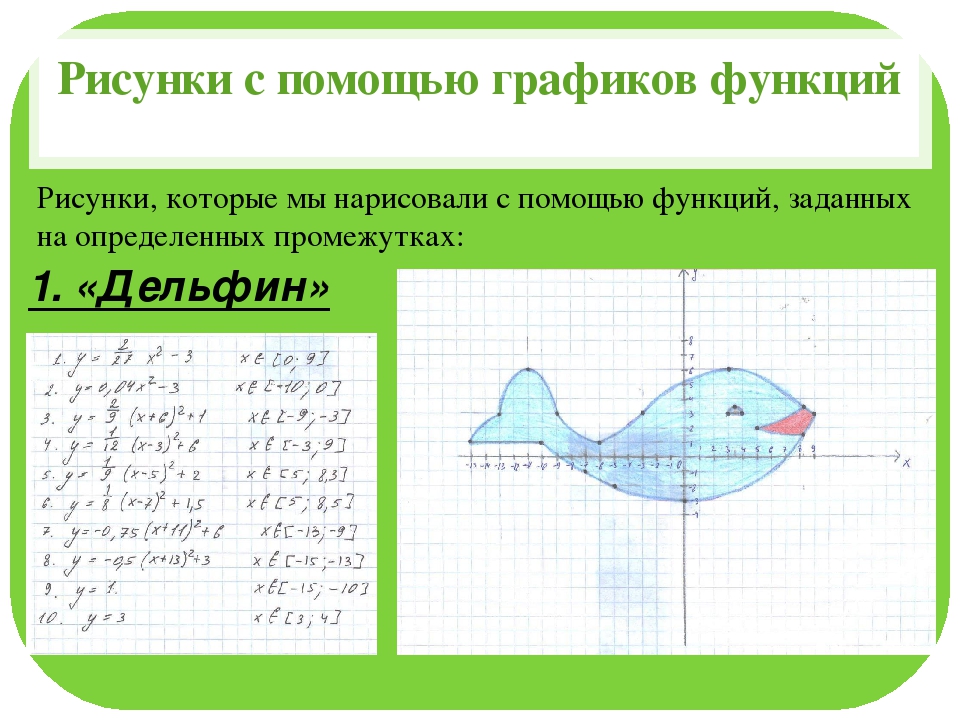 Объясняю что это значит: чтобы вычислить f1(n) нужно сначала вычислить f0(n), причем не просто вычислить а подставить саму в себя n-ное количесвто раз. Вот как это выглядит:
Объясняю что это значит: чтобы вычислить f1(n) нужно сначала вычислить f0(n), причем не просто вычислить а подставить саму в себя n-ное количесвто раз. Вот как это выглядит:
f1(1) = f0(1) = 1+1 = 2
f1(2) = f0(f0(2)) = (2+1)+1 = 4
f1(3) = f0(f0(f0(3))) = ((3+1)+1)+1 = 6
и т.д.
f1(n) = f0(f0(f0(…(n)…))) — n-вложений
Когда функцию нужно рекурсивно вложить саму в себя несколько раз, это обычно записывают так f n(). То есть мы можем более кратко записать: f1(n) = f0n(n). Так же выходит, что f1(n) эквивалентна дублированию, то есть f1(n) = 2⋅n, значит это одинаково быстрорастущие функции.
Идем дальше. Умножение растет еще быстрее: n⋅m, поскольку мы вольны умножать не только на 2, а на любое число. Возведение в квадрат имеет еще более быстрый рост, это происходит по той же причине, из-за которой дублирование растет быстрее сложения, банально, функции требуется всего один аргумент вместо двух: n2=n⋅n.
Ну а булеан 2n, если помните такую функцию по второй части, соответственно имеет еще более быстрый рост.
Здесь снова переходим к функциям быстрорастущей иерархии. Следующая на очереди f2(n), которая определяется так же рекурсивно f2(n) = f1n(n).
f2(n) = f1(f1(f1(…(n)…))) — n-вложений,
где каждый f1(n) = f0(f0(f0(…(n)…))) — n-вложений.
Иными словами мы уже имеем рекурсию внутри рекурсии. Вот так это рассчитывается:
f2(1) = f1(1) = f0(1) = 1+1 = 2
f2(2) = f1(f1(2)) = f1(f0(f0(2))) = f1(4) = f0(f0(f0(f0(4)))) = 8
f2(3) = f1(f1(f1(3))) = f1(f1(6)) = f1(12) = 24
f2(n) растет быстрее, чем булеан и равна 2n⋅n. n или n[6]n, и следом f5(n).
n или n[6]n, и следом f5(n).
И так далее по всему гипероператору. Мы даже можем вывести формулу:
fk(n) > n[k+1]n > n[k+1]m, которая справедлива в среднем по уровню роста, при разумных m.
Или fk(n) > 2[k+1]n, которая справедлива всегда.
Теперь внимание, мы переходим на новый уровень рекурсий. Как мы уже уяснили n[k]n быстрее n[k]m по скорости роста, при любом гипероператоре, начиная со сложения, умножения и так далее, потому что для роста функции нужно меньше аргументов. Это называется принцип диагонализации. Чтобы понять, что это означает, представьте себе таблицу умножения: в левом верхнем углу у нее находятся самые малые ее значения, а в правом нижнем углу самые большие. Кратчайший путь от самых малых до самых больших значений будет по диагонали, как раз по тому пути и проходит функция n⋅n. Этот же принцип можно применить и к функциям быстрорастущей иерархии: fn(n) будет расти быстрее, чем fk(n).
fn(n) это очень быстрорастущая функция. Она растет быстрее, чем гипероператор типа n[k]m, типа n[k]n и даже быстрее, чем n[n]n. Соотвественно она растет быстрее стрелочной нотации Кнута, которая отличается от гипероператора лишь: n↑km = n[k+2]m. Примерно с этой же скоростью растет функция Аккермана, очень важная функция из теории вычислимости, она определяется как A(n,m) = 2[m](n+3) — 3.
Функцию fn(n) принято обозначать как fω(n). Это всего лишь хитрый трюк. Из третьей части мы помним, что ω это первый трансфинитный ординал, обозначающий упорядоченность в бесконечности. Но в функциях быстрорастущей иерархии значек ω не связан с бесконечностью, он используется чтобы создавать диагонализационные рекурсии. Когда мы разбирали трансфинитные ординалы, вы должны были убедиться, что каждый ординал, который на порядок больше предыдущего, построен на новой рекурсии. Вот и математики решили, зачем изобретать велосипед, и позаимствовали эти рекурсии для функций быстрорастущей иерархии.
Теперь следите за тем, как создаются рекурсии на основе трансфинитных ординалов:
fω+1(n) = fω(fω(fω(…(n)…))) — n-вложений, или как мы уже знаем, более корректно это можно записать так fω+1(n) = fωn(n).
Это очень сильный скачек вперед. То есть в выражении fω(fω(n)) мы изначально вычисляем fω(n) = fn(n) а затем, внимание, fω(fn(n)) = ffn(n)(fn(n)).
Поэтому fω+1(n) растет намного быстрее, чем скажем fn[n]n(n). И уже такое число: fω+1(64) будет намного больше, чем Число Грэма.
Соотвественно, дальше идет:
fω+2(n) = fω+1(fω+1(fω+1(…(n)…))) — n-вложений, или fω+2(n) = fω+1n(n).
И уже где-то здесь по скорости роста расположилась моя функция superhyper(), которую мы использовали в предыдущих частях цикла.
fω(n) > superhyper(n,n,n)
fω+1(n) > superhyper(n,n,n,n)
fω+2(n) > superhyper(n,n,n,n,n)
fω+k(n) > superhyper(n,n,n,n,n,…) где k+3 аргумента функции
Переход на следующий уровень рекурсии выглядит так:
fω+n(n) = fω+ω(n) = fω⋅2(n)
Таковой будет скорость роста другой моей фунции quasi(), которая обобщает функцию superhyper(). А если точнее, то ее скорость будет даже такой: fω⋅2+3(n) > quasi(n,n)
На этом заканичваются масштабы, которые я еще как-то пытался визуализировать для читателя в первой части. В следующей пятой части мы будем разберирать еще более сильные нотации для записи чисел, которые уже не поддаются непосредственной визуализации, но вместо нее мы теперь можем использовать функции быстрорастущей иерархии.
Быстрорастущая иерархия
2.
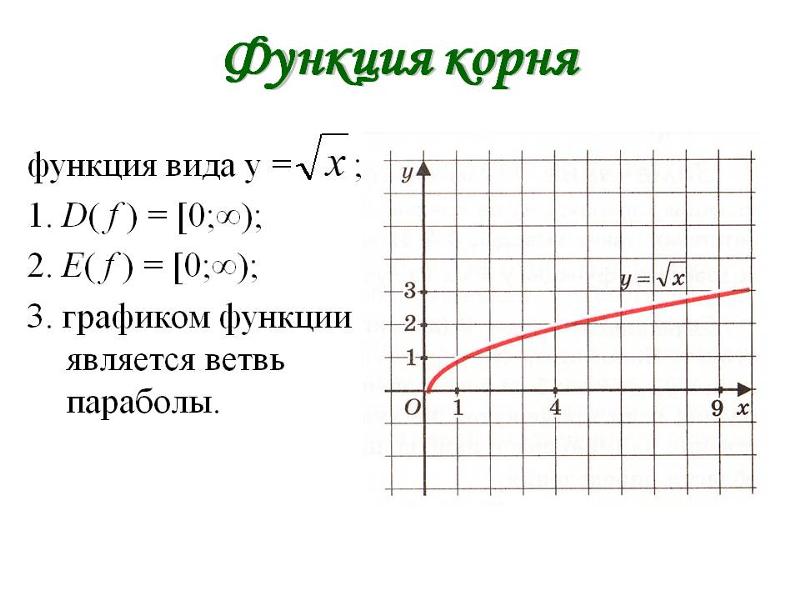 {М-1}11}.
{М-1}11}.Таким образом, первый трансфинитных порядковых ω {\свойства стиль отображения значение \омега } предел соответствует указатель нотации кнута.
Известный число Грэма менее f ω 1 64 {\свойства стиль отображения значение f_{\омега 1}64}.
Благодаря простоте и ясности в определении быстрорастущих иерархии используется для анализа различных нотаций для записи больших чисел.
Данное определение определяет быстрорастущих иерархии до ε 0 = ω ↑↑ n {\свойства стиль отображения значение \Попова закон нуля или единицы _{0}=\омега \стрелку вверх \стрелку вверх n}. для дальнейшего роста, вы можете использовать Веблен и другие, даже более мощные обозначений для ординалов.
| Краткое содержание | Старшее население — это самая быстрорастущая возрастная группа в мире, но она также и самая подвержены хроническим заболеваниям и инвалидности. Один из самых распространенных негативов Последствиями старения является снижение мышечной массы, силы и мощности. Это наиболее примечательно в мышцах нижних конечностей. Эти мышцы необходимы для выполнения повседневной деятельности. включая ходьбу, подъем по лестнице и вставание из положения сидя. Регулярные упражнения считается одним из самых эффективных способов замедлить и даже обратить вспять прогрессирование мышечная слабость. Тем не менее пожилые люди могут заметить снижение своей способности к выполнять регулярные упражнения, это может быть связано со снижением способности мышц буферизировать рН. Было высказано предположение, что карнозин (полученный путем связывания β-аланина и гистидина) способствует расширение физической работоспособности, противодействующее снижению способности мышц к буферный pH. Тем не менее, этот процесс буферизации pH в значительной степени ограничен количеством β-аланина. имеется в организме человека. β-аланин, как уже известно, снижается у пожилых людей из-за к сокращению пищевых продуктов (мясо, рыба, птица). Однако эти данные основаны на участниках, как молодых, так и пожилых, которые хорошо отдохнули. без предварительной тренировки или утомления оцениваемых мышц. Остается неясным, является ли β-аланин добавка поможет снизить уровень pH, когда мышцы уже утомлены. Таким образом, это исследование надеется изучить эффекты 4-недельного приема β-аланина. на сократительные и силовые свойства нижних конечностей, утомление до и после мышц. | Вмешательство | Тип вмешательства: Dietary Supplement Название вмешательства: beta-alanine Этикетка Arm Group: Beta-alanine supplementation Тип вмешательства: Пищевая добавка Название вмешательства: Плацебо Этикетка Arm Group: Плацебо | Приемлемость | Критерии: Критерии включения: — Все участники будут определены как «стабильные с медицинской точки зрения» для исследований физических упражнений, поскольку предложенный Grieg et al. (1994). Этот критерий был разработан как для безопасности, так и для определить степени свободы от болезней, которые могут повлиять на выполнение упражнений (Грейг и др., 1994). Критерий исключения: — Участники будут исключены, если они вегетарианцы / веганы или употребляли Добавки с β-аланином или креатином в течение последних 6 месяцев. Они также будут исключены если они участвовали в программе тренировок с отягощениями в течение последних 6 месяцев. Доказательство Биг-тета и других асимптотических определений (Биг-тета, Биг-Омега, Big-O, Литтл-тета, Литтл-омега) Поэтому в будущем задании я заметил некоторые проблемы, которые требовали от нас просто use этих правил. Мне было интересно, существуют ли какие-либо правила для Литтл-тета и Литтл-омега (используя… Что именно представляет собой большая not нотация? Я действительно запутался в различиях между big O, большой Омегой и большой тета-нотацией. Я понимаю, что big O-это верхняя граница, а большая Омега-нижняя, но что именно представляет собой большая… есть ли у каждого алгоритма большая Омега? есть ли у каждого алгоритма большая Омега? Возможно ли, чтобы алгоритмы имели как Big O, так и большую Омегу (но не равны друг другу — не большая тета) ? Например, Quicksort Big O — O (n log n), но… Есть ли какой-нибудь алгоритм, у которого big O и большая тета отличаются? Есть ли какой-нибудь алгоритм, у которого big O и большая тета отличаются? Я обнаружил, что они очень похожи и в то же время сбивают с толку. Big O,тета и омега нотации Я действительно запутался, что представляют собой big O,большая тета и большая омега: лучший случай, худший случай и средний случай или верхняя граница и нижняя граница. Если ответ-верхняя граница и… Big O и большая Омега-это одно и то же, но наоборот? Это правда? f(n) = O(g(n)) === g(n) = Omega(f(n)) В основном они взаимозаменяемы, потому что они противоположны? Итак, если F находится в Big O из G, то G-большая Омега F? Когда использовать нотацию big O и когда использовать большую тета-нотацию Я понимаю, что Big O-это верхняя граница, а большая тета-это жесткая граница, когда, например, мы рассматриваем функции f(n)=O(g(n)) или аналогично для большой теты. Но откуда мы знаем, что… Большая Омега и большая тета Такая функция, как f(n)=3n^2+2 , является O (n^2), потому что n^2-самый большой показатель в функции. Большая тета находится между big o и большой омегой или это одновременно big o и большая омега? Большая тета, которая говорит, что это и big o, и большая омега. Насколько я понимаю, big o-это верхняя граница, которая означает, что для любого большого входного сигнала сложность не должна… Самые быстрорастущие сектора мировой экономики в 2020 годуСамые быстрорастущие сектора мировой экономики в 2020 годуПо мере того, как мир становится всё более продвинутым и взаимосвязанным, новые и старые отрасли должны идти в ногу с последними требованиями. От услуг по 3D-печати до автономных подводных аппаратов — мы решили собрать десять самых быстрорастущих по темпам ростов доходов экономических направлений в 2020-м году. Данные основаны на нашем экспертном анализе и базе данных по более чем 70 мировым отраслям от сервиса IBISWorld. При анализе были использованы экономические, демографические и рыночные данные, а также прогностический подход. Производство респираторных вентиляторов. Прогнозируемый рост выручки в 2019-20 годах составит 54,8%. Продукция, производимая индустрией респираторных вентиляторов, долгое время была одним из основных продуктов в мировом секторе здравоохранения. Спрос на вентиляторы исторически был стабильным, поскольку они являются крайне важным спасительным средством для пациентов с ограниченной функцией дыхания. В спокойные времена больницам обычно не требуется значительное количество вентиляторов, но пандемия Covid-19 сформировала острую потребность и стремительный взлёт спроса на эту продукцию в 2020 году. Пациентам с тяжелыми симптомами коронавируса часто требуется вентиляция, потому что их лёгкие становятся настолько воспалёнными, что не способны больше обеспечить организм достаточным количеством кислорода. Хотя вентиляция не всегда успешна, на данном этапе развития терапии коронавируса она является единственным вариантом, который может поддерживать жизнь пациентов. Услуги 3D-печати и быстрого создания прототипов. Прогнозируемый рост выручки в 2019-20 годах составит 28,8%. Последние пять лет индустрия услуг 3D-печати и быстрого создания прототипов быстро развивалась, благодаря новым технологическим разработкам, снижению затрат и развитию программного обеспечения для технологии 3D-печати. Хотя падение цен на 3D-печатные машины побудило многие компании приобретать собственные машины и обходить отраслевые услуги, спрос, тем не менее, продолжает расти. В течение пяти лет, начиная с 2020 года, выручка отрасли будет расти в годовом исчислении на 27,3% и достигнет $309,9 млн к началу 2025 года. Рост индустрии будет тесно связан с расходами на исследования и разработки в производственном секторе. Большинство компаний используют 3D-печать для создания прототипов, потому что 3D-печать является очень эффективным процессом с экономической точки зрения. Сервисы по гидроразрыву пласта. Прогнозируемый рост выручки в 2019-20 годах составит 27,8%. Гидравлический разрыв пласта, обычно известный как фрекинг, представляет собой специализированный метод, используемый для извлечения сырой нефти и природного газа из недоступных сланцевых пластов. В сочетании с горизонтальным бурением, гидроразрыв пласта привёл к быстрому росту добычи нефти и природного газа в США в течение последних пяти лет. В течение этого периода, отрасль бурения и добычи нефти инвестировала значительный капитал в заключение контрактов на оказание услуг по гидроразрыву пласта для стимулирования добычи нефтяных и газовых скважин. В результате, например, только в 2015 году выручка отрасли выросла на 44%. Несмотря на крайне негативное влияние пандемии Covid-19 на нефтяную отрасль, ввиду долгосрочного характера контрактов, ожидается, что рост сервисов по гидроразрыву пласта продолжится и в этом году. Производство автономных подводных аппаратов. Прогнозируемый рост выручки в 2019-20 годах составит 26,7%. В последние годы в производстве автономных подводных аппаратов наблюдается устойчивый рост, при этом доходы отрасли в течение следующих 5 лет, по оценкам, будут расти в годовом исчислении на 23,5%, достигнув $885,4 млн. к 2025 году. Впервые разработанные в 1960-х годах, автономные подводные аппараты — это подводные суда, запрограммированные для выполнения поставленной задачи; они могут перемещаться независимо, со своим собственным источником питания. Эта промышленность генерирует большую часть своих доходов от военных заказов и рынка безопасности (наблюдение, разведка, противоминные меры и противолодочные войны). Многие автономные подводные аппараты всё ещё являются продуктами в стадии разработки, и внимание военных к этому продукту свидетельствует о будущем коммерческом потенциале роста. Тем не менее, доходы увеличились, поскольку вооруженные силы продолжают сохранять своё внимание на автономных подводных аппаратах. Магазины по продаже медицинской и рекреационной марихуаны. Прогнозируемый рост выручки в 2019-20 годах составит 25,2%. Индустрия медицинских и развлекательных магазинов марихуаны, в которую входят магазины, продающие розничную медицинскую марихуану (только по рецепту) и рекреационную марихуану, значительно расширилась за последние годы. В частности, избирательный цикл 2016 года обеспечил разгромные победы как для розничной торговли каннабисом, так и для медицинской. Следовательно, легализация марихуаны для медицинских и/или рекреационных целей и растущее её признание предоставили операторам и инвесторам беспрецедентные возможности для роста. В последние годы не было недостатка в спросе, поэтому индустрия каннабиса стала одной из самых быстрорастущих, особенно в Соединённых Штатах и Канаде. Массажные франшизы. Прогнозируемый рост выручки в 2019-20 годах составит 23,6%. Индустрия массажных франшиз включает в себя франчайзинговые магазины, которые предоставляют услуги лечебного и рекреационного массажа. Сервисы по доставке готовых блюд. Прогнозируемый рост выручки в 2019-20 годах составит 23,4%. В течение предыдущих пяти лет до 2020 года, отрасль услуг по доставке продуктов питания демонстрировала устойчивый рост, чему способствовал рост здорового образа жизни потребителей и устойчивый рост доли услуг, предоставляемых через интернет. Привязанность потребителей к интернету способствовала росту отрасли в этот период, особенно благодаря тому, что заказ набора из готовых блюд через интернет экономит время и упрощает процесс покупки и приготовления пищи. Растущий уровень располагаемого дохода позволил потребителям платить за наборы готовых блюд с предварительно порционированными ингредиентами, а лёгкий и приятный опыт таких покупок способствовал росту данной индустрии. Ожидается, что в течение пяти лет после 2020 года доходы отрасли возрастут в годовом исчислении на 20,9% до $3,5 млрд. Разработчики программного обеспечения для видеоконференций. Прогнозируемый рост выручки в 2019-20 годах составит 22,8%. Ожидается, что индустрия разработчиков программного обеспечения для видеоконференций в течение ближайших лет будет активно расширяться. Инструменты связи в мире всё в большей степени становятся незаменимыми для работы и непрерывной деятельности крупных организаций, особенно корпораций. Социальные сети. Прогнозируемый рост выручки в 2019-20 годах составит 19%. С тех пор, как пятнадцать лет назад они стали популярными, сотни миллионов людей по всему миру стали использовать социальные сети; от Facebook и Twitter до Instagram и десятков других, люди используют эти сети, поддерживают отношения с друзьями, следят за новостями и обмениваются фотографиями и видео. Используя пользовательские данные для целевых рекламных объявлений, при помощи которых получается подавляющее большинство доходов, операторы в сфере социальных сетей смогли извлечь выгоду из популярности своих платформ. Ожидается, что в течение следующих пяти лет, до 2025, года отрасль будет расти в годовом исчислении на 17,7% до $119,7 млрд. Данный сектор выигрывает от постоянного перетока расходов на рекламу в интернет и распространения мобильных устройств, подключённых к нему. Производство дезинфицирующих средств для рук. Прогнозируемый рост выручки в 2019-20 годах составит 18,7%. Компании из сектора дезинфицирующих средств для рук производят их в различных формах, таких как пена, гель, салфетки и жидкости, а также в виде дозаторов для промышленных продуктов. Доходы отрасли демонстрируют здоровый рост, увеличившись за прошлый год на 3,9% до $74,4 млн., но в 2020-ом году, из-за повышенного спроса в результате недавней вспышки коронавируса Covid-19, прогнозируемый рост сектора может составить до 18,7%. Пандемия Covid-19, безусловно, является главным событием этого года в мире. Она значительно повлияла на большинство аспектов повседневной жизни людей, поэтому неудивительно, что когда речь идёт о наиболее быстрорастущих экономических направлениях этого года, то на общем фоне выделяются сектор здравоохранения, а также направления, получившие ускорение роста доходов на фоне более широкого распространения удалённой работы. В каких-то секторах тенденции на сильный рост доходов будут устойчивыми, например, в сфере социальных сетей или программного обеспечения для видеоконференций, а в каких-то нет. К таким направлениям, скорее всего, можно отнести производство респираторных вентиляторов и дезинфицирующих средств для рук, но, по крайней мере в этом году, все вышеперечисленные сектора имеют возможность зафиксировать значительные темпы роста выручки и прибыли. Топ-10 самых быстрорастущих акций в мае От Investing.com© Reuters.Investing.com — После мартовского падения рынков, благодаря беспрецедентным фискальным стимулам центробанков по всему миру, фондовые рынки практически восстановились. Между ними удалось вклиниться привилегированным акциям «Ленэнерго (MCX:)», которые подорожали на 40,81% и заняли второе место. Как напоминает РБК, взлет цены произошел после того, как после двухмесячного перерыва, связанного с реорганизацией компании, акции вернулись на биржу 18 мая. На четвертом месте бумаги МОЭСК (+15,40%), на пятом — Селигдар (MCX:) (+14,37%), на шестом — ОГК-2 (MCX:) (+13,34%). Средний рост десяти лучших российских акций составил 21,04%. При этом мультипликаторы указывают, что акции «Россетей», МОЭСК и РусГидро перекуплены. Топ-10 американских акций по доходности в мае возглавил американский модный ритейлер L Brands, который владеет такими брендами как Victoria’s Secret и Bath & Body Works. Однако после того, как было объявлено о продаже Victoria’s Secret акции L Brands потеряли больше половины стоимости на фоне рушившегося рынка и упали ниже $10. Восстанавливаться акции начали после публикации отчетности, когда бренд косметики и парфюмерии Bath & Body Works продемонстрировал уверенный рост, хотя в целом квартал оказался убыточным. Тем не менее, к концу мая акции L Brands выросли на 36,16% до $16,2. Второе место иностранной части топа заняли акции китайского интернет-магазина JD.com. На фоне всеобщей самоизоляции покупки в интернете выросли и за май бумага показал рост на 26,06%. Третье место заняли акции платежной системы PayPal с ростом на 26,02%. Еще в апреле PayPal объявила о рекордном увеличении числа пользователей и объема платежей. А после публикации отчетности 6 мая акции PayPal ускорили рост. Рост популярности онлайн-платежей помог и сервису Square (NYSE:), который за месяц прибавил 24,47% и занял четвертое место в списке. Далее следуют NVIDIA (+21,47%), ViacomCBS (+20,16%), Cleveland-Cliffs (+19,18%), Baker Hughes (+18,35%), American International (+18,21), Ber Bath & Beyond (+17,45%). В среднем десять лучших акций, торгующихся на американских торговых площадках, подорожали за май на 22,75%. Мультипликаторы указывают, что переоцененными являются акции JD.com, Square и NVIDIA. Правда, эти бумаги могут считаться классическими акциями роста и могут продолжить расти.. Все еще недооцененными остаются бумаги ViacomCBS и American International. Самая быстрорастущая социальная сеть: что делать бизнесуВести Hi-Tech сообщают, что, согласно исследованию, в 2018-м году самым скачиваемым приложением из социальных сетей оказалась TikTok — бывшая Musical.ly. Основной контент в TikTok — короткие музыкальные видео, выкладываемые пользователями. Основной контент в TikTok — короткие музыкальные видеоПриложение могли скачивать чаще аналогов просто потому, что крупнейшие конкуренты уже присутствуют в телефонах большинства людей. Но не похоже, что это лишь эффект низкой базы. Общее количество скачиваний уже превысило 1 млрд. Причем, возможно, превысило существенно. «Статистика Sensor Tower включает только официальные данные Google Play и App Store. Сторонние Android-магазины, откуда скачивают приложения в Китае, где сервисы Google заблокированы, в расчет не берутся. Так что реально аудитория TikTok намного больше», — уточняется в сообщении Вести Hi-Tech. Также о серьезности претензий TikTok на позицию новой крупнейшей социальной платформы говорит статистика вовлеченности пользователей. Данные по США показывают, что пользователи проводят в приложении почти столько же времени, сколько пользователи Instagram (46 и 53 минуты в день соответственно). В России TikTok уже занимает уже 4-е место по показателю проводимого пользователями времени в приложении (после WhatsApp, ВКонтакте и Instagram). Какой интерес представляет TikTok для бизнесаСоциальные сети с высокой вовлеченностью интересны как место для присутствия бизнес-аккаунтов и размещения рекламы. В статье для Adindex.ru эксперт по маркетингу Александр Поляков рассказывает, как бренды могут использовать TikTok. Там наиболее эффективны вирусные маркетинговые компании, называемые «hashtag challenge». Для этого необходимо придумать хештег и добавить к нему креативное видео, призывающее всех увидевших поделиться чем-то похожим. Такой формат уже использовали Coca-Cola и бренд одежды Guess. Публикации пользователей в TikTok по хештегу #ShareaCoke (англ. — «поделись Колой»)В остальном работа с TikTok для бизнеса выглядит сложной, а польза неочевидна. Маркетологи в крупных компаниях пока заняли выжидательную позицию. Брендам трудно просто «присутствовать» из-за специфики контента, ведь самый популярный его вид — подпевание фоновой музыке. Тем не менее, в январе появились сообщения, что в TikTok замечена первая реклама. Пионером здесь стала американская GrubHub — сервис доставки еды из ресторанов. Реклама сервиса доставки еды Grubhub — одна из первых, появившихся в TikTok (англ. «Не выходя из дома», «Скачать приложение сейчас»).Хотя охват обещает быть большим в такой популярной соцсети, компаниям требуется совершенно другие типы креативного контента. Используемые в Instagram или Facebook тут не подойдут. Поэтому, не похоже, что продвижение через TikTok сейчас следует ставить в приоритет маркетинговой стратегии. Но, если хотите, то готовьте хештеги и выберите песню повеселее. О быстрорастущих вычислимых функцияхВведениеЭта страница вдохновлена концепцией асимптотической скорости роста функции. Асимптотическая скорость роста относится к поведению функции при неограниченно
большие значения его аргументов. Для функций f (n) одной переменной,
асимптотическая скорость роста относится к тому, насколько быстро f (n) растет с увеличением n без
связаны, по сравнению с другими функциями. Здесь мы фокусируем свое внимание в первую очередь на быстрорастущих функциях, поэтому мы пропустите некоторые общие функции, которые демонстрируют медленные темпы роста. Постоянные функцииПростейшей функцией является постоянная функция f (n) = C для некоторой постоянной число C. Это самый медленный темп роста: то есть вообще никакого роста. Линейные функцииЛинейные функции — это функции вида f (n) = An + B, где A и B — константы. Линейные функции — это «следующий шаг вперед» по сравнению с постоянными функции; они представляют собой линейную скорость роста. Линейные наросты характеризующийся тем, что изменение f (n) пропорционально изменению n. (Примечание: мы пропустили такие функции, как логарифмические функции и квадрат корневые функции, которые, строго говоря, находятся между постоянными функциями и линейные функции в терминах асимптотической скорости роста.Эти функции могут быть видно, что они возникают из инверсий быстрорастущих функций, которые мы обсуждаем ниже. Поскольку нас интересуют быстрорастущих -функций, мы не будем уделите гораздо больше внимания этим обратным функциям.) Квадратичные функцииКвадратичные функции имеют вид f (n) = An 2 + Bn + C, для некоторых константы A, B и C. Эти функции растут асимптотически быстрее, чем любые линейная функция. Поскольку квадратичный член An 2 доминирует над значением функции для больших значений n, мы считаем, что все квадратичные функции адекватно отраженный темпом роста функции возведения в квадрат Ан 2 . Учитывая быстрорастущую линейную функцию, такую как f (n) = 1000n, и скромно выглядящую
квадратичная функция g (n) = n 2 /1000, g в конечном итоге обгонит f, а f
никогда больше не догоню. Полиномиальные функцииЛинейные и квадратичные функции — лишь первые несколько членов большого класс полиномиальных функций. Полиномиальные функции имеют вид P (n) = C м n м + C м-1 n м-1 +… C 1 n + C 0 , где C 0 ,…, C м являются константы.По соглашению m выбирается так, чтобы C m было ненулевым. Мы затем назовите m градусов P и напишите deg (P) = m. Для наших целей мы действительно интересуют только многочлены с m≥1 и С м > 0. Когда m = 1, функция является линейной функцией, а когда m = 2, это квадратичная функция. функция. Легко видеть, что для двух полиномиальных функций P (n) и Q (n), P асимптотически растет быстрее, чем Q, если deg (P)> deg (Q), и наоборот. Так как этого свойства каждому многочлену может быть присвоено натуральное число, равное его степень, представляющая скорость его роста. Экспоненциальные функцииПростейшая экспоненциальная функция имеет вид f (n) = B n , для некоторая константа B. Мы называем B основанием экспоненциального члена В н. . Показательная функция доминирует над на каждые полиномиальной функции. Нет только она растет быстрее, чем линейная функция, квадратичная функция или четный g (n) = n 100000 ; он превосходит всех полиномиальных функций. Следовательно, мы можем рассматривать экспоненциальную функцию f (n) = B n как «Суперполином» бесконечной степени. Экспоненциальные функции не ограничиваются только B n . Например,
можно построить такие функции, как B n 2 , который растет быстрее
чем любая функция вида B n . Фактически, каждый непостоянный член в
показатель степени соответствует другому «уровню»
экспоненциальная функция, где более высокие уровни растут асимптотически быстрее, чем более низкие
уровни. Фактически, можно также построить вложенных экспонент с доминирующий член формы B B n , или B B B n . С точки зрения асимптотической скорости роста, эти функции лежат в верхних пределах класса экспоненциальных функции. Представительские функцииОбратите внимание, что, поскольку эти экспоненциальные функции доминируют над всеми полиномами функции, мы можем добавить полиномиальную функцию P (n) к экспоненциальной функции f (n) без существенного изменения его асимптотической скорости роста.Следовательно, когда f (n) — экспоненциальная функция, f (n) + P (n), как правило, будет иметь достаточно аналогичное поведение асимптотического роста с f (n), которое мы объединяем в одну и ту же категория. В общем, так же, как многочлен более высокой степени доминирует над всеми полиномы более низких степеней, так же как экспоненты доминируют над всеми полиномами, и так же, как вложенные экспоненты доминируют над всеми простыми экспонентами и экспоненты менее глубоко вложены, мы можем классифицировать функцию на основе термина или фактор, который больше всего способствует его асимптотической скорости роста. Например, поскольку b n доминирует над всеми многочленами, мы можем классифицировать все функции вида b n + P (n) для некоторого полинома P в того же класса, что и b n , и позвоните представителю b n функция в своем классе. Более того, поскольку факторы вида b b n доминирующие факторы вида b n , мы можем рассматривать все функции формы f (n) = b b n c n + P (n) как принадлежащие тому же класса, с представителем g (n) = b b n . С этого момента мы будем рассматривать все примеры функций как
относится к классам, к которым относится функция, за исключением случаев, когда контекст
указывает иное. Тетрациональные функцииЧтобы по-настоящему выйти за пределы класса экспоненциальных функций, нам нужно использовать арифметическая операция высшего порядка.Вложенные возведения в степень формы n n … n , где имеется m вхождений n, иногда называют опорными мощностями . Так же, как умножение повторное сложение и возведение в степень повторяется умножение, башни власти повторяются в возведении в степень и соответствуют следующему более высокому порядку операция. Эту операцию иногда называют тетрацией , от до подчеркнуть свое положение в последовательности сложение, умножение, возведение в степень,… . Существуют различные обозначения для обозначения тетрации, в том числе Стрелка вверх Кнута (n ↑↑ m) и левая рука Руди Ракера надстрочный индекс ( m n для n, преобразованного в m). Здесь мы примем более расширяемая нотация и напишите n (4) m вместо n, преобразованного в m. Функции вида f (n) = n (4) C для некоторой константы C соответствуют с вложенными экспоненциальными функциями. Эти функции доминируют менее глубоко вложенные (или не вложенные) экспоненциальные функции, но все же могут быть представлены используя только возведение в степень. Однако функции вида f (n) = B (4) n, для некоторой константы B, не могут быть представлены в виде вложенных экспонент с фиксированным числом вложений. Мы классифицируем эти функции как тетрациональных функций. Они доминируют над всеми экспоненциальными функциями, включая вложенные экспоненциальные функции с фиксированный уровень вложенности. Операционные функции высшего порядка Причина, по которой мы выбрали обозначение n (4) m для тетрации, заключается в том, что
мы можем повторить процесс диагонализации . Здесь очевидным становится ограничение обозначения стрелки вверх Кнута. К определить операции более высокого порядка, нам нужно использовать индексированный обозначение стрелки вверх.Мы определяем n (i) м как означающее n ↑ и-2 м. Операции (i) порождают иерархию арифметических
операции, известные как иерархия Гжегорчика . Для каждого i
function f (n) = B (i) n — функция, которая превосходит все функции
g (n) = C (j) n для j Функция АккерманаФункция Аккермана неизбежно встречается в процессе поиска все более быстрорастущие функции. Есть несколько разных определений, но все они воплощают одну и ту же основную концепцию. Одно определение:
Из этого определения может быть не сразу очевидно, что Аккерманн
функция представляет собой скорость асимптотического роста, превышающую каждые
операция высшего порядка в иерархии Гжегорчика, до тех пор, пока не будет предпринята попытка
вычислить его значения для различных значений m и n.Мы рассмотрим несколько небольших
значения m и n, чтобы проиллюстрировать его поведение. Для m = 0, если мы увеличим n от 0, мы увидим, что A (m, n) принимает значения 1, 2, 3, 4,… соответственно. Другими словами, A (0, n) = n + 1. Для m = 1, снова позволяя n перебирать первые несколько чисел, мы получаем значения 2, 3, 4, 5,…. Итак, A (1, n) = n + 2. Пока это кажется довольно ручным. Для m = 2, повторяя n через несколько первых чисел, мы получаем 3, 5, 7, 9, …. Итак, A (2, n) = 2n + 3. Лишь слабая тень грядущего. Пусть m = 3, и повторите n как обычно. Получаем 5, 13, 29, 61,…. Маленький Анализ показывает, что A (3, n) = 2 n + 3 -3. Теперь истинная сила Функция Аккермана начинает поднимать голову. Теперь пусть m = 4 и повторите n. Получаем 13 65533, а затем безмерно большой номер, а именно 2 65536 -3. Следующее за ним число настолько велико, что он легко переполняет типичные библиотеки программирования BigNum, предназначенные для обработки большое количество. Он равен 2 2 65536 -3, или, чтобы использовать тетрациональная запись, 2 (4) 6-3.В общем, А (4, п) = 2 (4) (п + 3) -3. В общем, значения A (5, n) слишком велики, чтобы их можно было вычислить даже с помощью современный компьютер с большим объемом памяти. При анализе выясняется, что А (5, п) = 2 (5) (п + 3) -3. В общем, A (m, n) = 2 (m) (n + 3) -3. Теперь определим функцию f (n) = A (n, n). Легко видеть, что это функция превзойдет всех функций, соответствующих более высокому порядку операции в иерархии Гжегорчика.Доминирующий фактор в любом из этих Последняя функция имеет вид b (i) n, где b и i являются постоянными. Но поскольку в f (n) преобладает член 2 (n) (n + 3) и n будет в конечном итоге превзойти константу i, f (n) в конечном итоге будет преобладать b (i) n для любой постоянной i. Следовательно, в некотором смысле f (n) может рассматриваться как соответствующая
операционная функция высшего порядка с бесконечным порядком. Помимо функции АккерманаФункция Аккермана далека от асимптотических темпов роста, достижимых рекурсивные (вычислимые) функции. Продолжить можно так: Определите итерацию функции для произвольной функции f следующим образом: f 1 (n) = f (n) Теперь, учитывая некоторую функцию f (n), определите связанную функцию @f следующим образом: @f 1 (n) = f n (n) Мы называем @f двойной диагонализацией f. Мы можем рассматривать @ как «оператор функции», который выполняет двойная диагонализация по ф. Например, возьмем функцию-последователь s (n) = n + 1. Тогда @s (n) = O (A (n)). Другими словами, @ преобразует функцию-преемник в что-то с асимптотической скоростью роста функции Аккермана. Очевидно, @ — очень мощный функциональный оператор; мы можем применить его несколько раз, чтобы получить к темпам роста, значительно превышающим функцию Аккермана. Согласимся, что когда мы пишем @@ f, мы имеем в виду @ (@ f), а когда мы пишем @@@ f, мы имеем в виду @ (@ (@ (f))) и так далее.Поскольку @s (n) имеет асимптотическую скорость роста функция Аккермана, @@ s (n) должна значительно превосходить функцию Аккермана. функция A (n). Он превосходит постоянные итерации A и (n), диагонализация A n (n), и даже постоянные итерации диагонализация, @A и (n). Обозначим @@ s (n) через B (n). B (n) = O (@A (n)). Мы можем производить еще более быстрорастущие функции, диагонализуя процесс применение самого @: пусть @ i f обозначает i применения @ к f.Это сказать: @ 1 f (n) = @f (n) Затем мы можем сформировать функцию g (n) = @ n f (n). Теперь мы можем диагонализовать процесс диагонализации приложений @ к функция. Определяем: #f 1 (n) = @ n s (n) Очевидно, этот процесс может продолжаться бесконечно: мы определяем новые функции и операторы над функциями, а затем операторы над операторами над функциями и т. д. Но чтобы сориентироваться в этом лесу, требуется какое-то центральное объединяющее понятие. Трансфинитные порядковые числаТеперь перейдем к предмету, который поначалу может показаться не связанным с тем, что мы обсуждали, но, как выяснилось, обеспечит центральную объединяющую понятие, которое мы ищем при построении все быстрее и быстрее растущих вычислимых функции. Трансфинитные порядковые числа являются обобщением конечных порядковых чисел (во-первых, второй, третий,…), чтобы включить нескончаемые числа. Ниже приводится определение порядковых чисел фон Неймана:
Порядковый номер α согласно этому определению является хорошо упорядоченным (поскольку множество сдерживание хорошо организовано, Аксиома Foundation), и это как раз тот набор, который содержит все ординалы меньшего размера чем себя.Если α конечно, то ему соответствует натуральное число n, и определяется как количество содержащихся в нем элементов. Таким образом, пустое множество ∅ = 0, {0} = 1, {0,1} = 2, {0,1,2} = 3,… и так далее. Набор натуральных чисел, который мы обозначим через ω, также является порядковый по этому определению, поскольку он содержит только ординалы (естественный чисел), и каждый элемент ω является подмножеством ω, а любой меньший элемент (при установленном отношении включения) также является элементом ω. Следовательно, ω — бесконечный (или трансфинитный ) ординал.Он находится в на самом деле, наименьший бесконечный ординал, поскольку он является супремумом всех (конечные) натуральные числа. Одно из важнейших свойств порядковых чисел, давших любой набор ординалов, объединение всех ординалов в наборе также порядковый номер, и является супремумом набора: это максимальный порядковый номер в наборе, если набор ограничен, и это наименьший ординал, содержащий ординалы в наборе, если набор неограничен. Например, если α = {2,5,6} = {{0,1}, {0,1,2,3,4}, {0,1,2,3,4,5}}, тогда объединение все элементы в α равны {0,1,2,3,4,5}, что равно 6 по определение. Порядковые номера преемниковДля любого ординала α можно составить множество β = α∪ {α}. Новый порядковый номер β называется преемником α, и обозначается α + 1. Например, 1 + 1 = {0} ∪ {{0}} = {0, {0}} = {0,1} = 2. Таким образом, мы можем определить операция-последователь s (α) = α∪ {α} для любого ординала α. Обратите внимание, что эта операция теперь применяется не только к натуральным числам, но и к бесконечные ординалы типа ω: ω + 1 определяются как ω∪ {ω} = {0,1,2,3,… ω}. Мы говорим, что порядковый номер α является порядковым номером преемника , если существует
существует ординал β такой, что α = β + 1. Порядковое добавлениеТеперь мы можем определить итеративную операцию-преемник: с 0 (α) = α Должно быть очевидно, что s i (α) = α + i. В его нынешнем виде это определение работает только для конечных ординалов i, но можно определить это также для трансфинита i. Мы просто расширили определение, включив в него то, что происходит при предельных порядковых номерах:
Обозначение ∪ γ <β s γ (α) означает совокупность всех ординалов, заданных как s γ (α), для все ординалы γ <β.Как мы упоминали ранее, объединение любого набора of ordinals также является порядковым номером, поэтому это гарантирует, что наш повторный преемник функция всегда создает порядковый номер. Это определение повторяющейся операции-преемника позволяет нам определить порядковое сложение для любых двух порядковых чисел α и β: α + β = с β (α) Обратите внимание, что, как правило, порядковое сложение не коммутативное : α + β — это , а не , равное β + α в целом. Это в отличие от сложения конечных чисел. Умножение порядковых чиселПовторяя операцию сложения, которую мы определили для порядковых чисел, мы может определять порядковое умножение:
Из этого определения легко увидеть, что a n (α) = α + α +… + α (n раз) для конечного n.Это также работает для трансфинитного n, такого как ω: a ω (α) является просто супремумом α⋅1, α⋅2, α⋅3, …. Следовательно, мы можем определить порядковое умножение так: α⋅β = а β (α) Порядковое возведение в степеньПорядковое возведение в степень можно построить аналогичным образом, повторяя порядковое умножение. Определение практически идентично:
Легко видеть, что m β (α) просто α умножается на себя в β раз; следовательно, мы можем определить порядковое возведение в степень как: α β = м β (α) За пределами порядкового возведения в степеньТеперь может возникнуть соблазн предположить, что мы можем определить порядковое тетрирование следующим образом: повторение порядкового возведения в степень, точно так же, как мы построили конечную тетрацию из конечное возведение в степень по итерации.Мы можем — но только до ω. Чтобы понять, почему это так, рассмотрим последовательность ω, ω ω , ω ω ω , …. Мы можем ограничиться этим процессом, чтобы получить порядковый номер, который содержит все такие «энергетические башни» из ω конечной высоты. Это порядковый номер Кантора ε 0 , который интуитивно соответствует к силовой башне бесконечной высоты. Мы можем думать об этом как о ω (4) ω, используя наши обозначения операций высшего порядка. До сих пор очень хорошо. Теперь возникает вопрос, как определить ω (4) (ω + 1)? Интуитивно говоря, знает , что это соответствует степени башня высотой ω + 1; но, к сожалению, этот не может быть определен в терминах повторяющихся экспонент.Причина в том, что возведение в степень неассоциативный: x y z не то же самое, что (x y ) z . Следовательно, учитывая силовую башню T = x x … x = x (4) n, T x равно , а не , равному x (4) (n + 1), но на самом деле намного меньше. Теперь — это , чтобы получить x (4) (n + 1), взяв x T вместо этого, и это то, что позволяет определить тетрацию в терминах повторяющихся экспонент конечной высоты . Однако это не распространяется на трансфинитные ординалы: в общем, порядковые операции не коммутативны , поэтому ω (4) (ω + 1) ≠ ω (4) (1 + ω). В На самом деле 1 + ω = ω. Итак, если мы попытаемся определить ω (4) (ω + 1) = ω ω (4) ω , мы понимаем, что он по-прежнему равен ω (4) ω = ε 0 . По факту, ε 0 — это , определенное Кантором как как наименьший порядковый номер. такой, что ω ε 0 = ε 0 . Проблема здесь в том, что для опор трансфинитной высоты добавление одного больше ω к основанию башни не увеличивает ее. Нам нужно добавить следующий ω к вершине башни. Однако вершина башня недостижима арифметически — бесконечная башня ω ω ω … не имеет вершины! Чтобы преодолеть эту проблему, нам нужно использовать другой подход. Порядковые фиксированные точкиФиксированная точка порядковой функции F — это порядковый номер α, такой что α = F (α).Например, рассмотрим s ‘(α) = 1 + α. (Примечание: это не то же самое, что функция-последователь s (α) = α + 1, которая имеет в ординалах нет неподвижных точек. Помните, что порядковая арифметика не коммутативен.) Если α конечно, то s ‘(α)> α. Однако если α = ω, тогда s ‘(α) = 1 + ω = ω = α. Следовательно, ω является неподвижной точкой s ‘. Фактически, каждый ординал после ω также является фиксированным точка s ‘. (Например, s ‘(ω + 1) = 1 + (ω + 1) = (1 + ω) + 1 = ω + 1.) Аналогично рассмотрим a ‘(α) = ω + α. Для малых значений α, a ‘увеличивает его на ω: a’ (0) = ω, a ‘(1) = ω + 1, a ‘(2) = ω + 2, и даже a’ (ω) = ω + ω, и а ‘(ω + ω) = ω + ω + ω = ω⋅3.Если мы продолжим чтобы повторить ‘, мы в конечном итоге достигаем фиксированной точки: а ‘(ω⋅ω) = ω + ω⋅ω = ω⋅ω. После этого каждый ординал, больший ω⋅ω, будет неподвижной точкой а ‘. Теперь рассмотрим m ‘(α) = ω⋅α. Для достаточно малых α, m ‘увеличивает его в ω раз. Например, m ‘(ω) = ω⋅ω, m ‘(ω⋅ω) = ω⋅ω⋅ω. В конце концов, мы находим что неподвижная точка m ‘равна ω ω . Здесь отметим, что не каждый порядковый номер после ω ω является фиксированной точкой m ‘; для Например, m ‘(ω ω +1) = ω⋅ (ω ω +1) = ω⋅ω ω + ω⋅1 = ω ω + ω ≠ ω ω .Фактически, следующий наименьший порядковый номер, являющийся фиксированной точкой m ‘, равен ω ω À2. Это потому, что m ‘(α + β) = ω⋅α + ω⋅β, поэтому для этого равняется α + β, оба α и β должны быть неподвижными точками m ‘. С ω ω — наименьшая фиксированная точка m ‘, следующая наименьшая фиксированная точка должна быть ω ω + ω ω = ω ω 2. Обратите внимание, что для каждого из этих примеров есть несколько фиксированных точек, и что перечисление фиксированных точек позволяет нам пройти мимо порядкового номера, в котором функция «застряла» на.Теперь применим это к повторному порядковому возведению в степень в чтобы пройти ε 0 . Порядковый номерПрежде всего, Кантор использовал фиксированные точки для определения своего ε-числа. Пусть e ‘(α) = ω α . потом ε β определяется как β ‘фиксированная точка е ‘. Мы уже видели ε 0 , первую фиксированную точку e ‘, которую мы интуитивно идентифицируем как ω (4) ω. Теперь мы будем использовать ε-числа Кантора для определения порядковой тетрации за пределами ω (4) ω. Вспомните, как мы пытались определить ω (4) (ω + 1), используя повторенное возведение в степень, но не смог пройти мимо ε 0 . Интуитивно, , однако, мы «знаем», что ω (4) (ω + 1) это просто силовая башня высотой ω + 1. Если представить себе укладку каждого из в этой башне по прямой, получим трансфинитную последовательность ω, ω, ω,…, ω, где последний ω находится в ω’я позиция строки. Теперь заметьте, что если мы добавим еще один ω к слева от этой последовательности, , мы получаем ту же последовательность. Другими словами, ω ω (4) (ω + 1) = ω (4) (ω + 1). Значит, это должно быть одно из произведений Кантора. ε-числа. Но какой именно? Рассмотрим ординалы вида ω (4) ω + α, где 0 <α <ω (4) ω. Четко, ω ω (4) ω + α = ω ω (4) ω ⋅ω α = ω (4) ω⋅ω α ≠ ω (4) ω. Аналогично для ординалов вида ω (4) ω⋅α, где 1 <α < ω (4) ω, имеем ω ω (4) ω⋅α = (ω ω (4) ω ) α = (ω (4) ω) α ≠ ω (4) ω⋅α.Более того, (ω (4) ω) α < ω (ω (4) ω) α для 1 < α <ω (4) ω. Как правило, любой порядковый номер между ω (4) ω и ω (4) (ω + 1) — некоторая комбинация порядковых чисел с добавлением, умножение и возведение в степень, но ни одно из них не является фиксированной точкой е ‘. Другими словами, ω (4) (ω + 1) является следующим наименьшим неподвижная точка е ‘. Это означает, что он должен быть равен ε 1 .Следовательно, мы можем определить ω (4) (ω + 1) = ε 1 . Аналогичное рассуждение покажет, что после ω (4) (ω + 1), следующий наименьший порядковый номер, являющийся фиксированной точкой е ‘, должен быть ω (4) (ω + 2). А раз так, то должно быть равно ε 2 . Теперь картина ясна: ω (4) (ω + α) = ε α . Обратите внимание, что при α ≥ ω⋅ω эта эквивалентность схлопывается до ε α = ω (4) α. Итак, мы успешно определили порядковую тетрацию. с ω в качестве левого аргумента. Порядковый номерВооружившись нашим определением порядковой тетрации, мы теперь рассмотрим, что происходит. если повторить тетрацию: ω (4) ω = ε 0 , ω (4) ω (4) ω = ω (5) 3 = ε ε 0 , ω (4) ω (4) ω (4) ω = ω (5) 4 = ε ε ε 0 ,… и т. д. Итак, мы можем определить порядковый номер пятиконечного правого аргумента как: ω (5) 1 = ω Если довести этот процесс до предела, получим η 0 = ω (5) ω, который обладает свойством η 0 = ε η 0 .Опять же, это свойство фиксированной точки. Это означает, что теперь мы можем перечислить неподвижные точки процесс ε-индексации, который по индукции позволяет определить порядковый номер Пентация произвольных правых аргументов. Другими словами, мы позволяем η α как α’-я неподвижная точка ε-индексирования и определим ω (5) (2 + α) быть η α . Дополнительный термин «2» нужен только для того, чтобы индексы хорошо выстраиваются при конечном α; как только мы доберемся до ω и дальше, это уже не актуально. Иерархия ВебленаМы могли бы продолжить таким образом определение операций более высокого порядка в Иерархия Гжегорчика для порядковых чисел, но мы могли бы также принять более надежную обозначение для перечисления этих функций с неподвижной точкой.Эти фиксированные точки функции порождают так называемую иерархию ординалов Веблена, которая, согласно наша схема определения порядковых операций с использованием фиксированных точек в конечном итоге верните нас в сферу быстрорастущих функций. Фактически, функции соответствующие ординалам в верхних слоях иерархии Веблена растут так быстро, что они далеко-далеко превосходят иерархию Гжегорчика, Аккермана функции, и практически все очевидные попытки обойти Функция Аккермана, включая наши предыдущие попытки определить операторы на функции и операторы над операторами над функциями и т. д.. Сначала определим функцию ψ, которая будет нумеровать ординалы в иерархии Веблена. Мы примем несколько иное определение, чем обозначение φ, обычно используемое для иерархии Веблена. Несмотря на начальные проявления, это обозначение фактически эквивалентно по выразительной силе к обозначению φ, как только мы дойдем до ψ ω и далее. Мы принять эти обозначения, чтобы в дальнейшем было удобнее определять Функция взрывающегося дерева , которая будет функциональным эквивалентом порядковый номер Фефермана-Шютте Γ 0 .Но сначала определение:
КредитыЭта страница была вдохновлена различными онлайн-ресурсами о больших, конечных естественных номера, в том числе следующие:
ATR0Начиная с этого момента, совокупность этих функций не может быть доказана в PA. ZFCЭти функции не могут быть доказаны тотальными в арифметической трансфинитной индукции, но считаются доказуемо полными в \ (\ textrm {ZFC} \). Это не означает, что совокупность фактически проверена, и на самом деле список содержит функции, совокупность или даже вычислимость которых неизвестны в текущем сообществе гугологов .Кроме того, \ (\ vartheta \) с входами больше \ (\ Omega_2 \) и \ (\ psi \) с входами больше \ (\ varepsilon _ {\ Omega _ {\ omega} +1} \) в оценках не указаны. (и, возможно, неточно определенных ) OCF, и, следовательно, эти оценки бессмысленны . Кроме того, другие оценки не обязательно проверяются и могут быть просто ожиданиями, т.е. предположительными без доказательств .
Более сильные теории множествЭти функции нельзя доказать тотально в \ (\ textrm {ZFC} \), но известно, что они доказуемо полны в более сильных теориях множеств. Невычислимые функцииЭти функции невычислимы и не могут быть оценены компьютерными программами за конечное время. ДругоеСледующие функции не являются отдельными картами:
Список литературыБыстрорастущие функции | Комплексное проективное 4-пространствоЭто первая из запланированных двух частей серии статей о быстрорастущих функциях. Первая часть («быстрорастущие функции») представит концепцию быстрорастущей иерархии функций, использует некоторые обозначения для представления больших чисел, сделает задачу краткого списка IMO бесконечно более сложной и решит ее с помощью упорядочивания ординала ε_0. Во второй части («действительно быстрорастущие функции») будут подробно описаны функции Харви Фридмана n и TREE , прежде чем исследовать модели вычислений, такие как машины Тьюринга и лямбда-исчисление, чтобы достичь и превзойти функцию занятого бобра Σ. Быстрорастущая иерархияМы определим последовательность быстрорастущих функций. Для относительно медленного старта давайте начнем с функции f _1 ( n ) = n +2.Применение f _1 к натуральным числам дает последовательность {3, 4, 5, 6, 7, 8,…}. Теперь мы используем так называемую рекурсию, чтобы немного ускорить процесс. Для каждого положительного целого числа α определим f _ (α + 1) ( n ) = f _α ( f _α ( f _α (… f _α (2)…))) , где имеется n −1 копий f _α. Чтобы избежать появления эллипсов, мы можем представить это как повторение f _ (α + 1) ( n +1) = f _α ( f _ (α + 1) ( n )) с начальное условие f_ α (1) = 2.2 (оценка справа налево) из n двоек. Используя обозначение Кнута, направленное вверх, это записывается как 2 ↑↑ n . Самые слабые верхние границы, встречающиеся в элементарной теории Рамсея (глава 3 MODA), такие как теорема Рамсея и теорема ван дер Вардена, соответствуют функциям на ранних стадиях этой иерархии (наивная граница для ван дер Вардена составляет примерно f _4, если я правильно помню). Самый большой полный граф, который может быть трехцветным без монохроматического треугольника, объект теории Рамсея Мы также получаем функции в теории Рамсея, которые растут быстрее, чем любая из этих функций.Во второй части (действительно быстрорастущие функции) я опишу функции Фридмана n и TREE , причем последняя работает намного быстрее, чем все, что описано в этой первой части. Монеты в коробкахНедавний вопрос на Международной математической олимпиаде включает последовательность из шести коробок, каждая из которых изначально содержит одну монету. Вам разрешено выполнять две разные операции:
|
|---|


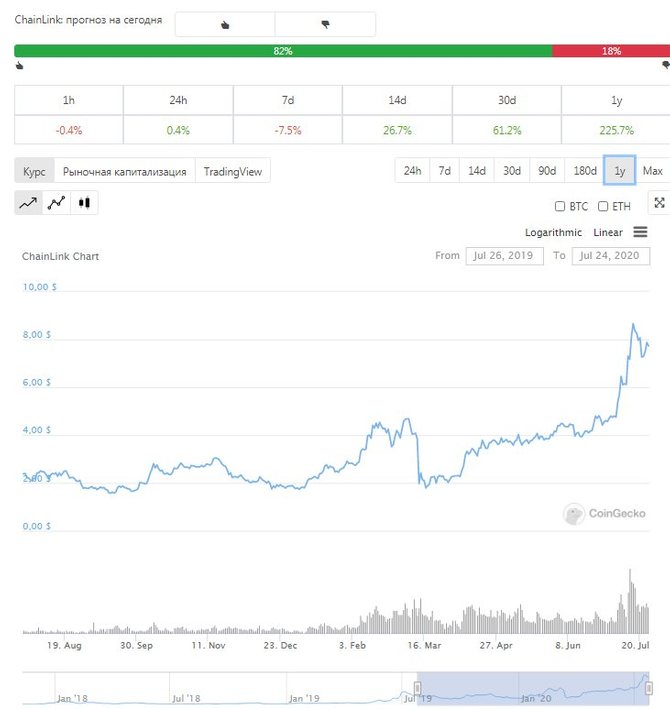 n…
n… 2) , потому что наибольший показатель степени равен…
2) , потому что наибольший показатель степени равен…

 Популярность массажных услуг выросла за последние годы, поскольку потребители всё чаще тратят излишки доходов на предметы роскоши. Кроме того, новые исследования, сообщающие о пользе для здоровья от массажа, также способствуют росту индустрии. Ожидается, что улучшение экономической обстановки и повышение узнаваемости массажных франшиз будут способствовать значительному росту этого сектора в течение будущих нескольких лет. Хотя большинство массажистов являются единоличными владельцами малого бизнеса, популярность массажных франшиз также выросла за последнее десятилетие. Франчайзи извлекают выгоду из эффективных операционных систем, систем поддержки, наряду с увеличением рекламы и узнаваемости бренда.
Популярность массажных услуг выросла за последние годы, поскольку потребители всё чаще тратят излишки доходов на предметы роскоши. Кроме того, новые исследования, сообщающие о пользе для здоровья от массажа, также способствуют росту индустрии. Ожидается, что улучшение экономической обстановки и повышение узнаваемости массажных франшиз будут способствовать значительному росту этого сектора в течение будущих нескольких лет. Хотя большинство массажистов являются единоличными владельцами малого бизнеса, популярность массажных франшиз также выросла за последнее десятилетие. Франчайзи извлекают выгоду из эффективных операционных систем, систем поддержки, наряду с увеличением рекламы и узнаваемости бренда. Эта тренд был поддержан несколькими ключевыми тенденциями, формирующими корпоративный ландшафт, включая высокоглобализированную рабочую силу, удалённую осуществление трудовых обязанностей и более плоские организационные структуры. Кроме того, функциональность и доступность программного обеспечения для проведения видеоконференций значительно улучшилась, поскольку за этот период был достигнут прогресс, как в программном, так и в аппаратном обеспечении. Эта стабильная функциональность и более высокая степень интеграции способствовали популяризации унифицированных коммуникаций.
Эта тренд был поддержан несколькими ключевыми тенденциями, формирующими корпоративный ландшафт, включая высокоглобализированную рабочую силу, удалённую осуществление трудовых обязанностей и более плоские организационные структуры. Кроме того, функциональность и доступность программного обеспечения для проведения видеоконференций значительно улучшилась, поскольку за этот период был достигнут прогресс, как в программном, так и в аппаратном обеспечении. Эта стабильная функциональность и более высокая степень интеграции способствовали популяризации унифицированных коммуникаций.
 «Обычка» «Россететй» заняла третье место в списке с ростом 28,84%.
«Обычка» «Россететй» заняла третье место в списке с ростом 28,84%.
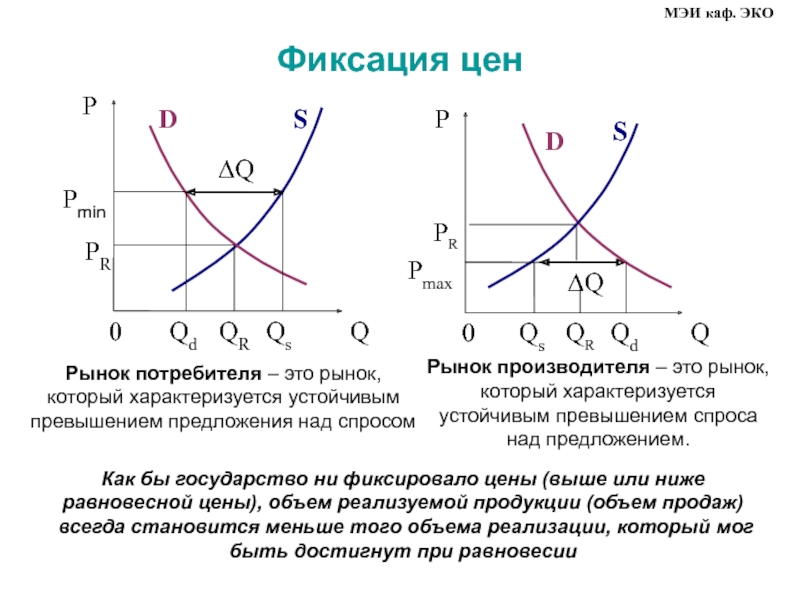
 Мы говорим, что функция f (n) имеет большее
асимптотический рост, чем функция g (n), или, что то же самое, f (n) доминирует над g (n), если для достаточно большого n f (n)> g (n).Более
именно «достаточно большой» означает, что n> M для некоторого фиксированного
постоянное значение M, определяемое относительно как f, так и g.
Мы говорим, что функция f (n) имеет большее
асимптотический рост, чем функция g (n), или, что то же самое, f (n) доминирует над g (n), если для достаточно большого n f (n)> g (n).Более
именно «достаточно большой» означает, что n> M для некоторого фиксированного
постоянное значение M, определяемое относительно как f, так и g.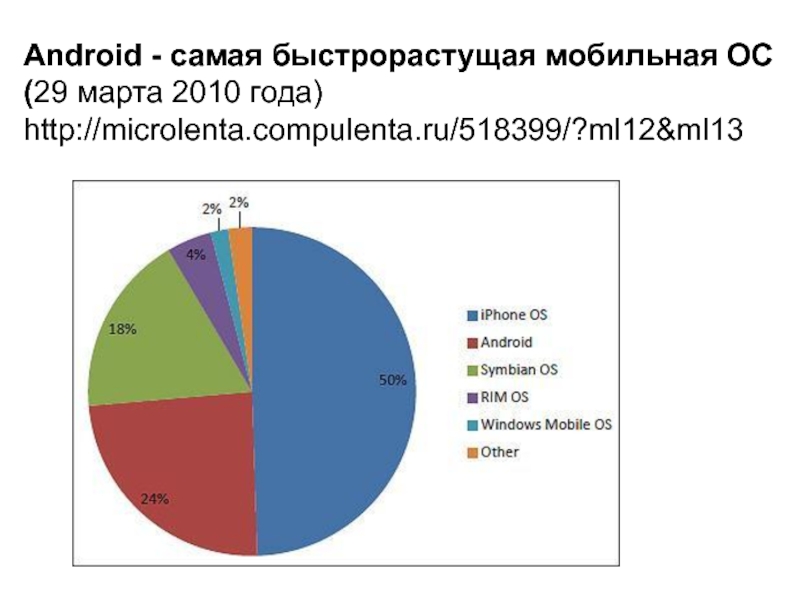 Это верно независимо от того, насколько велик коэффициент f
имеет, и независимо от того, насколько мал коэффициент g, пока он не
нуль.
Это верно независимо от того, насколько велик коэффициент f
имеет, и независимо от того, насколько мал коэффициент g, пока он не
нуль.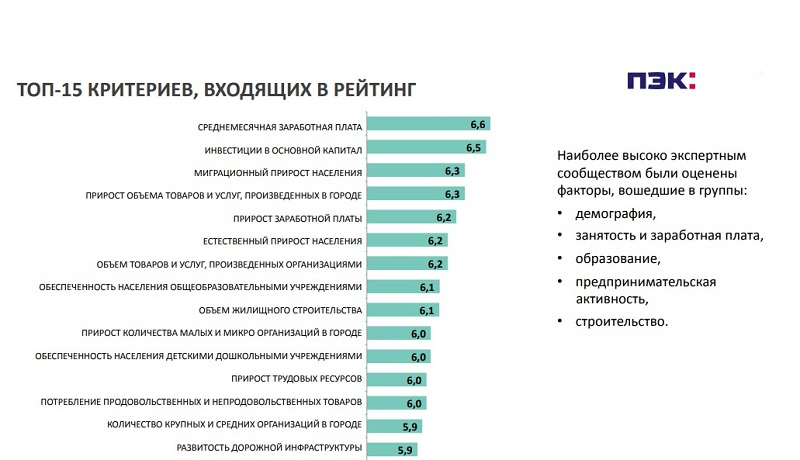 Например, B n 2 + n растет быстрее, чем
В № 2 .
Например, B n 2 + n растет быстрее, чем
В № 2 .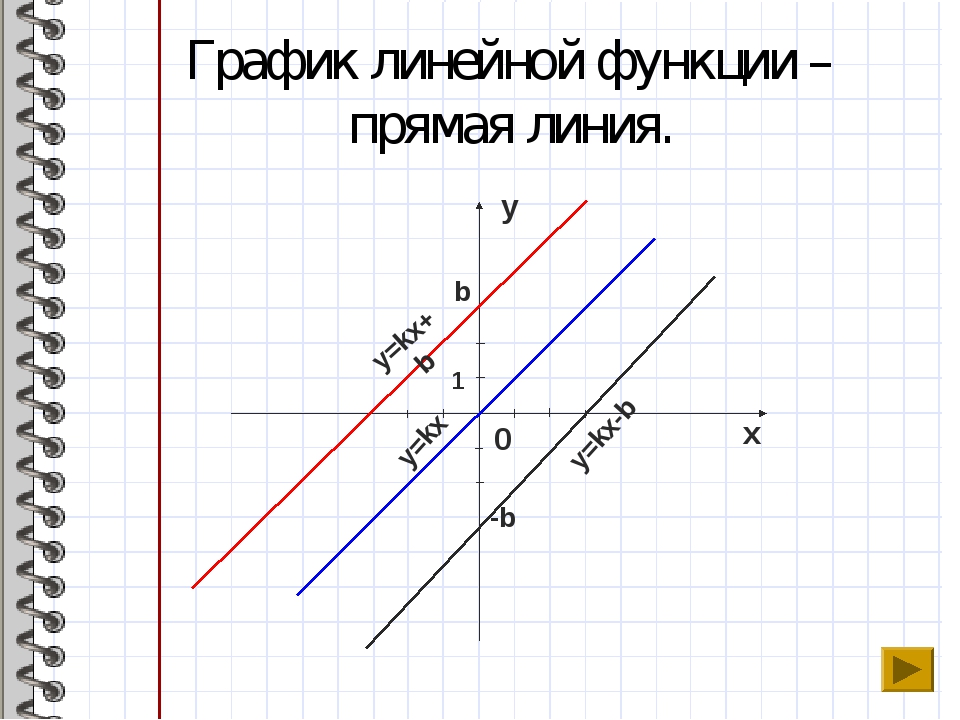 Следовательно, когда мы говорим об экспонентах f (n) = b n ,
следует понимать, что все функции образуются путем алгебраического комбинирования
f (n) с другими функциями с меньшей асимптотической скоростью роста.
Следовательно, когда мы говорим об экспонентах f (n) = b n ,
следует понимать, что все функции образуются путем алгебраического комбинирования
f (n) с другими функциями с меньшей асимптотической скоростью роста.
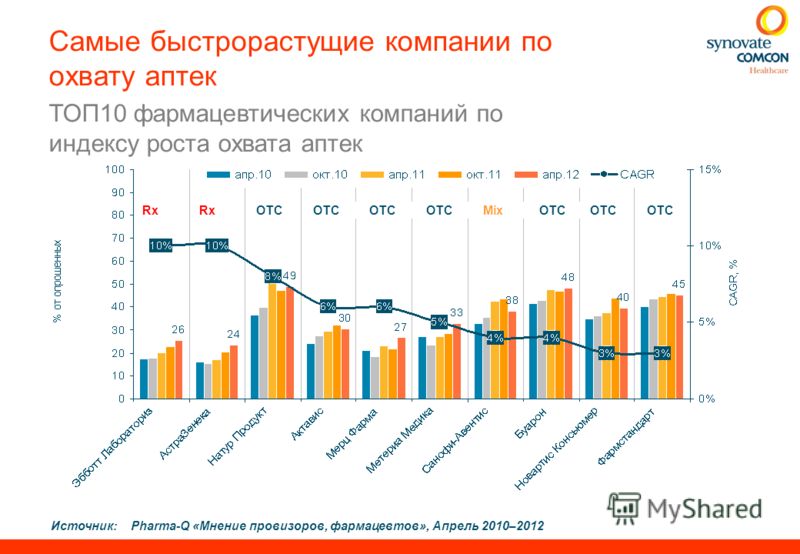 С этого момента для
для удобства мы будем писать A (n) для обозначения унарной функции Аккермана
f (n) = A (n, n).
С этого момента для
для удобства мы будем писать A (n) для обозначения унарной функции Аккермана
f (n) = A (n, n). Эта функция будет
превзойти все конечные применения @ к f. Если мы затем определим
C (n) = @ n s (n), мы получаем функцию, которая превосходит все
конечные приложения @ к функции Аккермана. Это эквивалентно
говоря, что это выходит за рамки всех конечных применений @ к функции-преемнику
s (n), поскольку @s (n) имеет эквивалентную скорость роста, что и A (n) — добавляя
эквивалент еще одного применения @ не меняет того факта, что любой
в конечном числе приложений @ будет преобладать C (n).
Эта функция будет
превзойти все конечные применения @ к f. Если мы затем определим
C (n) = @ n s (n), мы получаем функцию, которая превосходит все
конечные приложения @ к функции Аккермана. Это эквивалентно
говоря, что это выходит за рамки всех конечных применений @ к функции-преемнику
s (n), поскольку @s (n) имеет эквивалентную скорость роста, что и A (n) — добавляя
эквивалент еще одного применения @ не меняет того факта, что любой
в конечном числе приложений @ будет преобладать C (n).
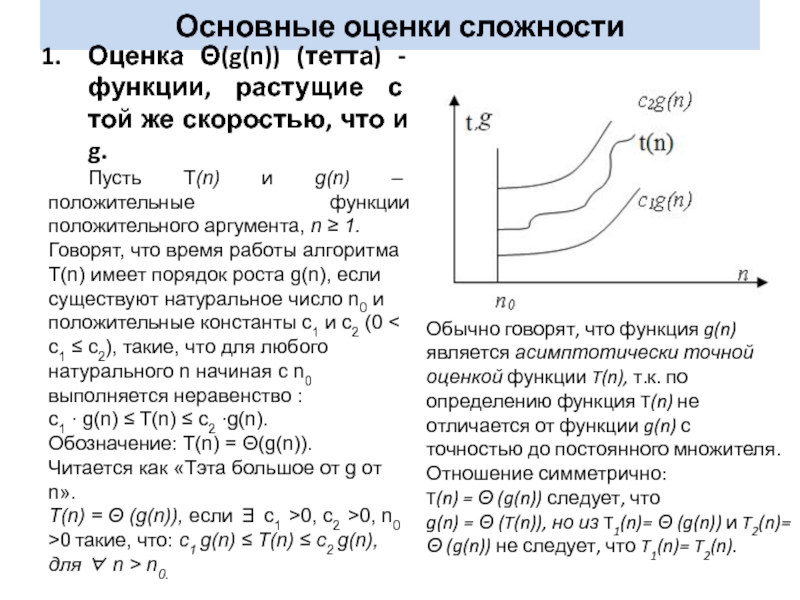 Если нет такого
β, то мы говорим, что α — предельный ординал . Другими словами,
предельный порядковый номер — это порядковый номер, который не может быть получен из предыдущих порядковых номеров с помощью
повторные применения функции-преемника s. Ноль такой предел
порядковый, потому что перед нулем нет порядковых. Бесконечный порядковый
ω — еще один предельный ординал: он не может быть получен из любого конечного ординала.
повторными применениями с. Это может быть достигнуто только «
fiat », взяв объединение всех натуральных чисел.
Если нет такого
β, то мы говорим, что α — предельный ординал . Другими словами,
предельный порядковый номер — это порядковый номер, который не может быть получен из предыдущих порядковых номеров с помощью
повторные применения функции-преемника s. Ноль такой предел
порядковый, потому что перед нулем нет порядковых. Бесконечный порядковый
ω — еще один предельный ординал: он не может быть получен из любого конечного ординала.
повторными применениями с. Это может быть достигнуто только «
fiat », взяв объединение всех натуральных чисел.