Формула для расчета массы: Формула массы тела в физике
В классической механике считают:
- масса тела не является зависимой от движения тела, от воздействия других тел, расположения тела;
- выполняется закон сохранения массы: масса замкнутой механической системы тел неизменна во времени.
Инертная масса
Свойство инертности материальной точки состоит в том, что если на точку действует внешняя сила, то у нее возникает конечное по модулю ускорение. Если внешних воздействий нет, то в инерциальной системе отсчета тело находится в состоянии покоя или движется равномерно и прямолинейно. Масса входит во второй закон Ньютона:
$$\bar{F}=m \bar{a}(2)$$где масса определяет инертные свойства материальной точки (инертная масса).
Гравитационная масса
Масса материальной точки входит в закон всемирного тяготения, при этом она определяет гравитационные свойства данной точки.при этом она носит название гравитационной (тяжелой) массы.
Эмпирически получено, что для всех тел отношения инертных масс к гравитационным являются одинаковыми.
Слишком сложно?
Формула массы тела не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Какова масса 2м3 меди?
Решение. Будем считать, что медь однородна и для решения задачи используем формулу:
$$m=\rho V$$При этом если известно вещество (медь), то можно при помощи справочника найти ее плотность. Плотность меди будем считать равной $\rho$ Cu=8900 кг/м3 . Для расчета все величины известны. Проведем вычисления:
$m=8900 \cdot 2=17800$ (кг)
Ответ. $m=8900 \cdot 2=17800$ (кг)
Читать дальше: Формула момента силы.
Формулы для вычисления массы тел различной формы
9.05.2013 // Владимир ТруновЭто странное название статьи объясняется только тем, что детали одной и той же формы могут быть как сплошными, так и полыми (т.е. следующая статья будет называться «Масса полой детали»).
Тут самое время вспомнить, что масса тела — это его объем , умноженный на плотность его материала (см. таблицы плотностей):
Объем сплошной детали — это… ее объем и больше ничего.
Примечание
Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.
Рассмотрим несколько простых форм (более сложные, как вы помните, можно составить путем сложения или вычитания простых).
1. Масса параллелепипеда (бруска)
Объем параллелепипеда: , где — длина, — ширина, — высота.
Тогда масса:
2. Масса цилиндра
Объем цилиндра: , где — диаметр основания, — высота цилиндра.
Тогда масса:
3. Масса шара
Объем шара: , где — диаметр шара.
Тогда масса:
4. Масса сегмента шара
Объем сегмента шара: , где — диаметр основания сегмента, — высота сегмента.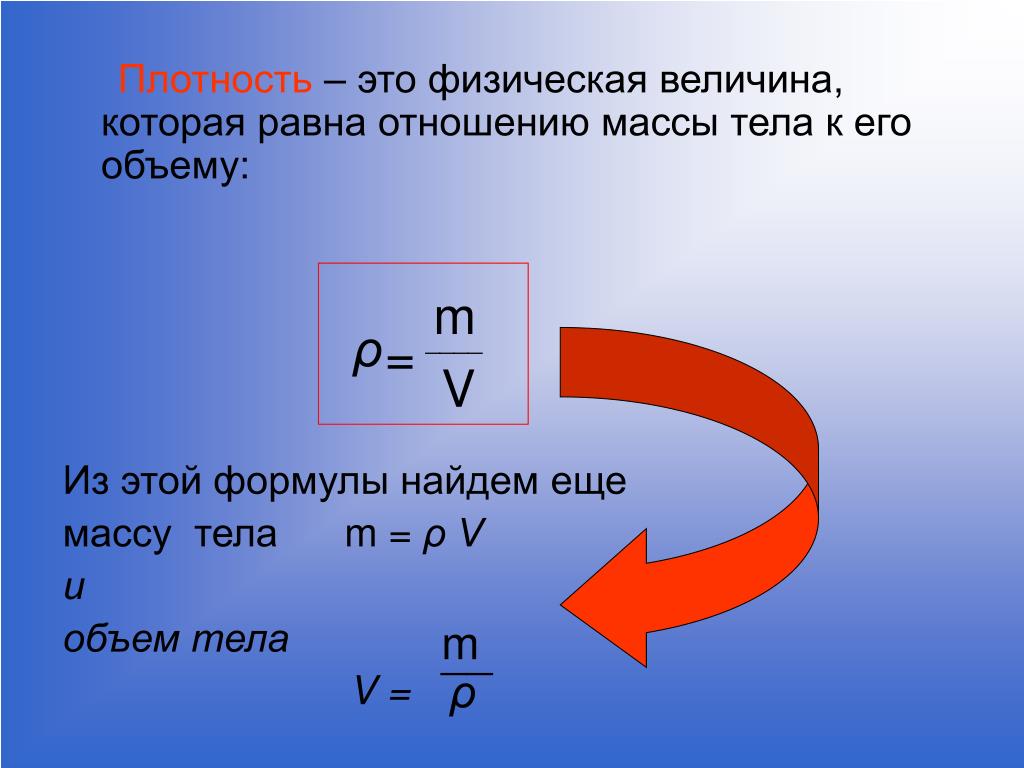
Тогда масса:
5. Масса конуса
Объем любого конуса: , где — площадь основания, — высота конуса.
Для круглого конуса: , где — диаметр основания, — высота конуса.
Масса круглого конуса:
6. Масса усеченного конуса
Поскольку невозможно объять необъятное, рассмотрим только круглый усеченный конус. Его объем — это разность объемов двух вложенных конусов: с основаниями и : , где , . После никому не интересных алгебраических преобразований получаем:
, где — диаметр большего основания, — диаметр меньшего основания, — высота усеченного конуса.
7. Масса пирамиды
Объем любой пирамиды равен одной трети произведения площади ее основания на высоту (то же самое, что и для конусов (часто мы не замечаем, насколько мироздание к нам благосклонно)): , где — площадь основания, — высота пирамиды.
Для пирамиды с прямоугольным основанием: , где — ширина, — длина, — высота пирамиды.
Тогда масса пирамиды:
8.
 Масса усеченной пирамиды
Масса усеченной пирамидыРассмотрим усеченную пирамиду с прямоугольным основанием. Ее объем — это разность объемов двух подобных пирамид с основаниями и : , где , .
Исчеркав половину тетрадного листа, получаем: , где , — ширина и длина большего основания, , — ширина и длина меньшего основания, — высота пирамиды.
И, оставив в покое остальную половину листа, исходя из одних соображений симметрии, мы можем написать еще одну формулу, которая отличается от предыдущей только заменой W на L и наоборот. В чем разница между длиной и шириной? Только в том, что мы их так назвали. Назовем наоборот и получим: .
или
Для пирамиды с квадратным основанием (, ) формула выглядит проще:
Расчет индекса массы тела — Центр диагностики и сердечно-сосудистой хирургии
Индекс массы тела — ИМТ (англ. body mass index (BMI)) — величина, позволяющая оценить степень соответствия массы человека и его роста и тем самым, косвенно, оценить, является ли масса недостаточной, нормальной, избыточной (ожирение).
где
- m — масса тела в килограммах,
- h — рост в метрах
и измеряется в кг/м2.
Показатель индекса массы тела разработан бельгийским социологом и статистиком Адольфом Кетле (Adolphe Quetelet) в 1869 году.
В соответствии с рекомендациями ВОЗ разработана следующая интерпретация показателей ИМТ:
| Индекс массы тела | Соответствие между массой человека и его ростом |
|---|---|
| менее 16.5 | Выраженный дефицит массы |
| 16.5—18.49 | Недостаточная (дефицит) масса тела |
| 18.5—24.99 | Норма |
25—29. 99 99 | Избыточная масса тела (предожирение) |
| 30—34.99 | Ожирение первой степени |
| 35—39.99 | Ожирение второй степени |
| 40 и более | Ожирение третьей степени (морбидное) |
Индекс массы тела следует применять с осторожностью, исключительно для ориентировочной оценки — например, попытка оценить с его помощью телосложение профессиональных спортсменов может дать неверный результат (высокое значение индекса в этом случае объясняется развитой мускулатурой).
Расчет количества продукта по данным раствора другого вещества.
Для расчета массы (объема, количества вещества) продукта реакции, если данные по одному из веществ представлены в виде раствора с определенной массовой долей этого растворенного вещества, следует воспользоваться нижеследующим алгоритмом:
1) Прежде всего следует найти массу растворенного вещества. Возможны две ситуации:
Возможны две ситуации:
* В условии даны масса раствора и массовая доля растворенного вещества (концентрация). В этом случае масса растворенного вещества рассчитывается по формуле:
* В условии даны объем раствора вещества, плотность этого раствора и массовая доля растворенного вещества в этом растворе. В таком случае следует воспользоваться формулой для расчета массы раствора:
После чего следует рассчитать массу растворенного вещества по формуле 1.
2) Рассчитать количество вещества (моль) участника реакции, масса которого стала известна из расчетов выше. Для этого воспользоваться формулой:
3) Записать уравнение реакции и убедиться в правильности расставленных коэффициентов.
4) Рассчитать количество моль интересующего участника реакции исходя из известного количества другого участника реакции, зная, что количества веществ любых двух участников реакции A и B относятся друг к другу как коэффициенты перед этими же веществами в уравнении реакции, то есть:
Если в условии требовалось рассчитать количество вещества, то действия на этом заканчиваются. Если же требуется найти его массу или объем, следует переходить к следующему пункту.
Если же требуется найти его массу или объем, следует переходить к следующему пункту.
5) Зная количество вещества, определенное в п.4, мы можем рассчитать его массу по формуле:
Также, если вещество является газообразным и речь идет о нормальных условиях (н.у.), его объем может быть рассчитан по формуле:
Рассмотрим пару примеров расчетных задач по этой теме.
Пример 1
Рассчитайте массу осадка, который образуется при добавлении к 147 г 20%-ного раствора серной кислоты избытка раствора нитрата бария.
Решение:
1) Рассчитаем массу чистой серной кислоты:
m(H2SO4) = w(H2SO4) ∙ m(р-ра H2SO4)/100% = 147 г ∙ 20% /100% = 29,4 г
2) Рассчитаем количество вещества (моль) серной кислоты:
n(H2SO4) = m(H2SO4) / M(H2SO4) = 29,4 г/98 г/моль = 0,3 моль.
3) Запишем уравнение взаимодействия серной кислоты с нитратом бария:
H2SO4 + Ba(NO3)2 = BaSO4↓ + 2HNO3
4) В результате расчетов стало известно количество вещества серной кислоты. Осадок представляет собой сульфат бария. Зная, что:
Осадок представляет собой сульфат бария. Зная, что:
n(BaSO4)/n(H2SO4) = k(BaSO4)/k(H2SO4), где n — количество вещества, а k — коэффициент в уравнении реакции,
можем записать:
n(BaSO4) = n(H2SO4) ∙ k(H2SO4)/k(BaSO4) = 0,3 моль ∙ 1/1 = 0,3 моль
5) Тогда масса осадка, т.е. сульфата бария, может быть рассчитана следующим образом:
m(BaSO4) = M(BaSO4) ∙ n(BaSO4) = 233 г/моль ∙ 0,3 моль = 69,9 г
Пример 2
Какой объем газа (н.у.) выделится при растворении необходимого количества сульфида железа (II) в 20%-ном растворе соляной кислоты с плотностью 1,1 г/мл и объемом 83 мл.
Решение:
1) Рассчитаем массу раствора соляной кислоты:
m(р-ра HCl) = V(р-ра HCl) ∙ ρ(р-ра HCl) = 83 мл ∙ 1,1 г/мл = 91,3 г
Далее рассчитаем массу чистого хлороводорода, входящего в состав кислоты:
m(HCl) = m(р-ра HCl) ∙ w(HCl)/100% = 91,3 г ∙ 20%/100% = 18,26 г
2) Рассчитаем количество вещества хлороводорода:
n(HCl) = m(HCl)/M(HCl) = 18,26 г/36,5 г/моль = 0,5 моль;
3) Запишем уравнение реакции сульфида железа (II) с соляной кислотой:
FeS + 2HCl = FeCl2 + H2S↑
4) Исходя из уравнения реакции следует, что количество прореагировавшей соляной кислоты с количеством выделившегося сероводорода связано соотношением:
n(HCl)/n(H2S) = 2/1, где 2 и 1 — коэффициенты перед HCl и и H2S соответственно
Следовательно:
n(H2S) = n(HCl)/2 = 0,5/2 = 0,25 моль
5) Объем любого газа, находящегося при нормальных условиях, можно рассчитать по формуле V(газа) = Vm ∙ n(газа), тогда:
V(H2S) = Vm ∙ n(H2S) = 22,4 л/моль ∙ 0,25 моль = 5,6 л
Формулы для решения задач по химии
от 01. 01.2017 года
01.2017 года
Настоящее пользовательское (лицензионное) соглашение (далее – «Соглашение») заключается между Обществом с ограниченной ответственностью «АЛЕКТА» (далее – «Лицензиар»), и Пользователем (физическим лицом, выступающем в роли конечного потребителя Продукта) совместно именуемые «Стороны».
Пожалуйста, внимательно ознакомьтесь с текстом настоящего Соглашения. Оно представляет собой публичную оферту и, после его принятия Вами, образует соглашение между Вами (Пользователем) и Лицензиаром о предмете и на условиях, изложенных в тексте Соглашения.
Принимая настоящее Соглашение, Вы соглашаетесь с положениями, принципами, а также соответствующими условиями лицензионного соглашения, изложенными ниже.
1. ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ
1.1. Программный продукт — экземпляры программы для ЭВМ «ХиШник», состоящей
из Серверной части (свидетельство о государственной регистрации базы данных
№2014621526) и Клиентского приложения (свидетельство о государственной
регистрации программы для ЭВМ № 2014661592), права на использование которой
предоставляются в соответствии с настоящим Соглашением.
1.2. Серверная часть — часть Программного продукта, размещенная в сети Интернет и
используемая для хранения данных в базе данных Лицензиара под наименованием
«ХиШник» (далее также – «база данных»), а также для хранения, обработки,
передачи данных Пользователя между базой данных и клиентским приложением.
1.4. Пользовательское (лицензионное) соглашение – текст настоящего Соглашения со всеми дополнениями, изменениями, приложениями к нему, размещенный на сайте Лицензиара и доступный в сети интернет по адресу: http://www.hishnik-school.ru
 5. Заключение Пользовательского (лицензионного) соглашения (акцепт
публичной оферты) — полное и безоговорочное принятие условий настоящего
Соглашения Пользователем путем совершения Пользователем одного (или
нескольких) из следующих действий:
5. Заключение Пользовательского (лицензионного) соглашения (акцепт
публичной оферты) — полное и безоговорочное принятие условий настоящего
Соглашения Пользователем путем совершения Пользователем одного (или
нескольких) из следующих действий: прохождение регистрации и (или) авторизации на Сайте Лицензиара в установленном им порядке;
внесение платежа за предоставление права на использование Программного продукта;
начало использования Пользователем Программного продукта в любой иной форме.
1.6. Лицензиар — сторона в настоящем Соглашении, обладающая исключительным правом на Программный продукт и предоставляющая по настоящему Соглашению Пользователю право использования Программного продукта, в пределах и способами, указанными в настоящем Соглашении.
1.
 7. Пользователь — физическое лицо, которое устанавливает на компьютер или
мобильное устройство Клиентское приложение и использует его.
7. Пользователь — физическое лицо, которое устанавливает на компьютер или
мобильное устройство Клиентское приложение и использует его. 1.8. Неисключительная лицензия — лицензионный договор, предусматривающий предоставление права использования Программного продукта с сохранением за Лицензиаром права заключения лицензионного договора с другими лицами.
1.9. Роль – набор функций, которые доступны в Программном продукте Пользователю. Настоящим Соглашением предусмотрены следующие роли:
1.9.1. Администратор — сотрудник образовательного учреждения, осуществляющий регистрацию и предоставление доступа к Программному продукту Пользователям – участникам образовательного процесса в образовательном учреждении.
1.9.2. Преподаватель – сотрудник образовательного учреждения, организующий и осуществляющий образовательный процесс посредством использования функций Программного продукта.
1.9.3. Репетитор – преподаватель, дающий частные уроки, может проводить как индивидуальные, так и групповые занятия посредством использования функций Системы вне рамок Образовательного учреждения.
1.9.4. Учащийся – обучающийся в Образовательном учреждении и (или) вне его, получающий и проверяющий свои знания посредством Системы.
1.10. Профиль — запись в базе данных, содержащая идентифицирующие сведения о Пользователе и его роли.
1.11. Демонстрационный режим – режим использования Программного продукта для целей ознакомления с его функциональными возможностями.
1.12. Продуктивный режим – режим использования Программного продукта для целей применения в образовательном процессе.
1.13. Регистрационный ключ — набор цифр и букв, посредством которого Пользователь получает право использования Программного продукта в Продуктивном режиме с полным доступом к Серверной части.

1.14. Логин – уникальный идентификатор Пользователя в базе данных.
1.15. Пароль – набор цифр и букв, посредством которого и совместно с Логином Пользователь получает доступ в Клиентское приложение Программного продукта.
1.16. Интернет сайт Лицензиара — http://www.hishnik-school.ru.
1.17. Контент — все объекты, размещенные на Сайте и в Программном продукте, в том числе элементы дизайна, текст, графические изображения, иллюстрации, видео, скрипты, программы, музыка, звуки и другие объекты и их подборки.
2. ПРЕДМЕТ СОГЛАШЕНИЯ
2.1. Лицензиар предоставляет Пользователю право использования Программного продукта «ХиШник» на условиях простой (неисключительной) лицензии в пределах и способами, указанными в настоящем Соглашении, а Пользователь обязуется уплатить Лицензиару вознаграждение за предоставление права использования Программного продукта в соответствии с условиями настоящего Соглашения.

2.2. Лицензиар гарантирует, что он является правообладателем исключительных прав на Программный продукт и имеет права на заключение Соглашения. Лицензиару в настоящий момент в соответствии с тем знанием, которым он обладает, не известны права третьих лиц, нарушаемые данным Соглашением.
2.3. Пользователь не вправе полностью или частично предоставлять (передавать) права третьим лицам, полученные им по Соглашению, в том числе продавать, тиражировать, копировать Программный продукт, предоставлять доступ третьим лицам, отчуждать иным образом, в т.ч. безвозмездно, без получения на все вышеперечисленные действия предварительного письменного согласия Лицензиара.
2.4. Соглашение предоставляет Пользователю право использования Программного продукта с сохранением за Лицензиаром права выдачи лицензий другим лицам.
 Пользователь может использовать экземпляр Программного продукта только в
пределах тех прав и теми способами, которые предусмотрены Соглашением.
Предоставляемое Пользователю Лицензиаром право на использование
Программного продукта действует в течение срока действия Соглашения.
Пользователь может использовать экземпляр Программного продукта только в
пределах тех прав и теми способами, которые предусмотрены Соглашением.
Предоставляемое Пользователю Лицензиаром право на использование
Программного продукта действует в течение срока действия Соглашения. 2.5. Программный продукт «ХиШник», состоящий из Серверной части и Клиентского приложения, представляет собой программу для ЭВМ, предназначенную для осуществления образовательного процесса.
2.6. Право использования Программного продукта (неисключительная лицензия), предоставляемое Пользователю в соответствии с настоящим Соглашением, включает право на использование Программного продукта в двух режимах:
2.6.1. Демонстрационный режим, ограниченный правом установки на компьютер или мобильное устройство, запуска, настройки Клиентского приложения и ограниченного доступа к Серверной части, для целей ознакомления с функциональными возможностями Программного продукта.
2.6.2. Продуктивный режим, ограниченный правом установки на компьютер или мобильное устройство, запуска, настройки Клиентского приложения и полного доступа к Серверной части, для целей применения Программного продукта в образовательном процессе.
2.7. Право использования Программного продукта предоставляется:
2.7.1. В демонстрационном режиме — с момента установки Клиентского приложения на компьютер или мобильное устройство.
2.7.2. В продуктивном режиме — с момента поступления денежных средств на счет Лицензиара.
2.8. Права на использование Программного продукта считаются предоставленными Пользователю:
2.8.1. В демонстрационном режиме — в момент установки Клиентского приложения на компьютер или мобильное устройство.
2.8.2. В продуктивном режиме — в момент направления Пользователю на электронную почту письма с регистрационным ключом.

2.9. Право использования Программного продукта предоставляется как на территории Российской Федерации, так и на территории всех иных стран мира, если не противоречит национальному законодательству этих стран.
2.10. Требования к компьютерам (оборудованию), необходимому для функционирования Клиентского приложения размещены в сети Интернет на сайте Лицензиара.
3. СТОИМОСТЬ И ПОРЯДОК ОПЛАТЫ
3.1. Размер вознаграждения Лицензиара за предоставление Пользователю прав на продуктивное использование Программного продукта размещен на Сайте Лицензиара.
3.2. Вознаграждение Лицензиара за предоставление прав продуктивного использования Программного продукта не облагаются НДС на основании подпункта 26 пункта 2 статьи 149 Налогового кодекса РФ.
3.3. Оплата предоставленных прав за продуктивное использование Программного продукта по настоящему Соглашению производится Пользователем в форме ежегодных платежей.

3.4. Способ оплаты по Соглашению: безналичное перечисление Пользователем денежных средств в валюте Российской Федерации (рубль) на расчетный счет Лицензиара способами, обозначенными на Сайте Лицензиара. При этом обязанность Пользователя в части оплаты вознаграждения по Соглашению считается исполненной со дня зачисления денежных средств банком на счет Лицензиара.
3.5. Лицензиар имеет право на одностороннее изменение условий и размера вознаграждения по настоящему Соглашению. Актуальный размер вознаграждения публикуется на Сайте Лицензиара.
4. СРОК ДЕЙСТВИЯ СОГЛАШЕНИЯ
4.1. Настоящее Соглашение вступает в силу с момента его заключения в соответствии с п.2.7.
4.2. Срок предоставления права продуктивного использования Программного продукта в соответствии с Соглашением составляет 1 (Один) год с момента авторизации Пользователя посредством Регистрационного ключа.
 Соглашение считается
заключенным на тех же условиях на новый срок, равный 1 (Одному) году, при
условии осуществления Пользователем полной оплаты за продление права
продуктивного использования Программного продукта. Количество пролонгаций не
ограничивается.
Соглашение считается
заключенным на тех же условиях на новый срок, равный 1 (Одному) году, при
условии осуществления Пользователем полной оплаты за продление права
продуктивного использования Программного продукта. Количество пролонгаций не
ограничивается. 4.3. Предоставление права демонстрационного использования Программного продукта не ограничен по сроку.
4.4. Расторжение настоящего Соглашения возможно в соответствии с условиями, указанным в действующем законодательстве РФ.
5. ПРАВА И ОБЯЗАННОСТИ СТОРОН
5.1. Пользователь обязуется:
5.1.1. Соблюдать права Лицензиара на Программный продукт и не использовать Программный продукт иными способами кроме тех, что предусмотрены настоящим Соглашением.
5.1.2. Не предпринимать попыток получения исходного кода Программного продукта для дальнейшего его использования, а также не извлекать материалы базы данных.

5.1.3. Своевременно уплачивать Лицензиару вознаграждение за предоставление Пользователю права продуктивного использования Программного продукта в порядке и сроки, установленные настоящим Соглашением.
5.1.4. Указывать достоверную информацию, в том числе свой адрес электронной почты и иные данные, запрашиваемые Лицензиаром. При этом в случае указания Пользователем недостоверной информации, все возможные риски, которые могут возникнуть в связи с выполнением настоящего Соглашения, Пользователь принимает на себя.
5.1.5. Строго придерживаться и не нарушать условий Соглашения, а также обеспечить конфиденциальность коммерческой и технической информации Лицензиара.
5.1.6. Не устанавливать Программный продукт на компьютерах (оборудованиях), не соответствующих техническим требованиям для функционирования Программного продукта.

5.1.7. Заботиться о том, чтобы права Лицензиара на Программный продукт не были нарушены третьими лицами на территории действия настоящего Соглашения, и обязан сообщить Лицензиару обо всех ставших ему известными нарушениях.
5.2. Пользователь вправе:
5.2.1. Использовать Программный продукт только посредством установки (записи) Клиентского приложения Программного продукта на компьютер или мобильное устройство и его настройки для осуществления ознакомительного или образовательного процесса с помощью базы данных.
5.2.2. Использовать Программный продукт для любых целей Пользователя, за исключением ограничений, определенных Соглашением.
5.3. Лицензиар обязуется:
5.3.1. Обеспечить технические условия функционирования Серверной части и Клиентского приложения для использования Программного продукта Пользователем, в том числе обеспечить возможность получения и/или предоставить дистрибутив (установочные файлы) Клиентского приложения, с помощью которого осуществляется использование Программного продукта.

5.3.2. Защищать данные Пользователя, которые стали известны Лицензиару в связи с исполнением Сторонами своих обязательств в соответствии с настоящим Соглашением.
5.3.3. Уведомлять Пользователя о невозможности использования Программного продукта в связи с выполнением сервисных работ не менее чем за 48 (Сорок восемь) часов путем отправки сообщения на электронную почту, указанную при регистрации.
5.3.4. Воздерживаться от каких-либо действий, способных затруднить осуществление Пользователя предоставленного ему права использования Программного продукта в установленных Соглашением пределах.
5.3.5. Предоставлять новые версии (обновления) Программного продукта путем их размещения в сети Интернет на сайте Лицензиара либо в системе Google Play с возможностью скачивания.
5.
 3.6. Информировать Пользователя о новых версиях (обновлениях) Программного
продукта, посредством направления уведомления на адрес электронной почты
Пользователя, указанный при регистрации и (или) авторизации на Сайте
Лицензиара.
3.6. Информировать Пользователя о новых версиях (обновлениях) Программного
продукта, посредством направления уведомления на адрес электронной почты
Пользователя, указанный при регистрации и (или) авторизации на Сайте
Лицензиара. 5.3.7. Обеспечивать круглосуточный прием обращений в Службу поддержки по адресу электронной почты: [email protected].
5.3.8. Осуществлять обработку поступивших обращений и консультации через Службу поддержки, в период с 5:00 до 14:00 по московскому времени с понедельника по пятницу, за исключением выходных и праздничных дней.
5.4. Лицензиар вправе:
5.4.1. Производить сервисные работы, которые могут повлечь перерывы в работе Клиентского приложения.
5.4.2. В случае нарушения Пользователем условий (способов) использования прав на Программный продукт в соответствии с настоящим Соглашением, лишить Пользователя лицензии на использование прав на Программный продукт путем закрытия доступа к Программному продукту.

5.4.3. Изменять в одностороннем порядке условия настоящего Соглашения в установленном порядке.
5.4.4. Отказаться в одностороннем порядке от исполнения Соглашения в порядке, предусмотренном применимым правом и/или настоящим Соглашением;
5.4.5. Осуществлять иные права, предусмотренные применимым правом, а также настоящим Соглашением.
6. ПОРЯДОК ИСПОЛЬЗОВАНИЯ ПРОГРАММНОГО ПРОДУКТА
6.1. Пользователю для использования Программного продукта предлагается установить (записать в память ЭВМ) и запустить Клиентское приложение Лицензиара, экземпляр которого скачивается Пользователем самостоятельно одним из следующих способов:
в сети Интернет на сайте Лицензиара;
в системе Google Play;
с флэш-накопителя, предоставленного Лицензиаром (опция).

6.2. После установки (записи в память ЭВМ) и запуска Клиентского приложения Лицензиара Пользователю предоставляется право использования Программного продукта в Демонстрационном режиме.
6.3. Для использования Программного продукта в Продуктивном режиме Пользователю необходимо в Клиентском приложении ввести Регистрационный ключ, который Лицензиар направляет Пользователю на адрес электронной почты, указанный на Сайте Лицензиара в запросе на предоставление доступа. Пользователь самостоятельно осуществляет использование Программного продукта путем запуска и настройки Клиентского приложения.
6.4. Программный продукт предоставляется Пользователю по принципу «as is» («как есть»), что подразумевает: Пользователю известны важнейшие функциональные свойства продукта, в отношении которого предоставляются права на использование, Пользователь несет риск соответствия Программного продукта его желаниям и потребностям, а также риск соответствия условий и объема предоставляемых прав своим желаниям и потребностям. Лицензиар не несет ответственность за какие-либо убытки или ущерб, независимо от причин их возникновения (включая особый, случайный или косвенный ущерб; убытки, связанные с недополученной прибылью, прерыванием коммерческой или производственной деятельности, утратой деловой информации, небрежностью, или какие-либо иные убытки), возникшие вследствие использования или невозможности использования Программного продукта.
6.5. Программный продукт предназначен для личных, образовательных и иных не связанных с осуществлением предпринимательской деятельности нужд физических лиц. Использование Программного продукта в коммерческих целях не допускается.
7. ОТВЕТСТВЕННОСТЬ СТОРОН
7.1. За невыполнение или ненадлежащее выполнение обязательств по настоящему Соглашению Стороны несут ответственность в соответствии с действующим законодательством, если иное не установлено Соглашением.
7.2. Стороны освобождаются от ответственности за неисполнение (ненадлежащее исполнение) Соглашения, если такое неисполнение (ненадлежащее исполнение) явилось следствием действий обстоятельств непреодолимой силы, наступление которых Стороны не могли предвидеть и предотвратить. Сторона, для которой надлежащее исполнение обязательства стало невозможным ввиду действия обстоятельств непреодолимой силы, обязана незамедлительно уведомить об этом другую Сторону. Стороны вправе ссылаться на действия обстоятельств непреодолимой силы лишь при условии, что они сделали все возможное в целях предотвращения и/или минимизации негативных последствий действия указанных обстоятельств.
7.3. Лицензиар не гарантирует абсолютную бесперебойность использования Программного продукта и не дает гарантию того, что произведенные третьими лицами программы для ЭВМ или любые другие средства, используемые при работе Программного продукта, абсолютно защищены от компьютерных вирусов и других вредоносных компонентов. Лицензиар обязуется осуществить все разумные меры для защиты информации Пользователя и обеспечения бесперебойного использования Программного продукта.
7.4. Пользователь самостоятельно отвечает за содержание информации, передаваемой им или иным лицом по сети Интернет и хранимой в памяти сервера Лицензиара, в том числе за ее достоверность и правомерность ее хранения и распространения.
7.5. В случае привлечения Лицензиара к ответственности или наложения на него взыскания в связи с допущенными Пользователем нарушениями прав третьих лиц, а равно установленных законодательством запретов или ограничений, Пользователь обязан в полном объеме возместить убытки Лицензиара.
7.6. В случае нарушения Пользователем условий и ограничений настоящего Соглашения, он является нарушителем исключительного права на Программный продукт. За нарушение авторских прав на Программный продукт Пользователь несет ответственность в соответствии с законодательством Российской Федерации.
7.7. Совокупная кумулятивная ответственность Лицензиара перед Пользователем в отношении требований любого рода, возникающих из настоящего Соглашения, не будет превышать сумму вознаграждения по данному Соглашению, фактически выплаченного Пользователем за Программный продукт, в отношении которого возникло требование, в течение 12 (двенадцати) месяцев, предшествующих возникновению требования. Вышеуказанные ограничения ответственности применяются даже в том случае, если с помощью вышеуказанного способа защиты права не удается добиться его основной цели.
8. ПЕРСОНАЛЬНЫЕ ДАННЫЕ
8.1. Информация, предоставленная Пользователем является конфиденциальной.
8.2. Предоставляя свои персональные данные Лицензиару, Пользователь соглашается на их обработку, как с использованием средств автоматизации, так и без использования средств автоматизации, в частности сбор, хранение, передачу третьим лицам и использование информации Лицензиаром в целях исполнения обязательств перед Пользователем в соответствии с настоящим Соглашением; получения Пользователем персонализированной рекламы; проверки, исследования и анализа данных, позволяющих поддерживать и улучшать Программный продукт.
8.3. Лицензиар обязуется не разглашать полученную от Пользователя информацию. Не считается нарушением предоставление Лицензиаром информации, в том числе персональные данные Пользователя третьим лицам, действующим на основании договора с Лицензиаром, в целях исполнения настоящего Соглашения.
8.4. Не считается нарушением обязательств по неразглашению информации предоставленной Пользователем, в том числе персональные данные Пользователя, в целях обеспечения соблюдения требований действующего законодательства Российской Федерации (в том числе в целях предупреждения и/или пресечения незаконных и/или противоправных действий Пользователей).
8.5. Пользователь не имеет права передавать свои Логин и Пароль третьим лицам.
8.6. Пользователь обязуется обеспечивать конфиденциальность своего Логина и Пароля и несет ответственность за использование Логина и Пароля третьими лицами. Ни при каких обстоятельствах Лицензиар не несет ответственность за использование третьими лицами Логина и пароля Пользователя.
8.7. В случае несанкционированного доступа к логину и паролю и/или персональной странице Пользователя, или распространения логина и пароля Пользователь обязан незамедлительно сообщить об этом Лицензиару посредством заполнения формы обратной связи, представленной на Сайте.
8.8. Лицензиар не несет ответственности за использование кем бы то ни было общедоступных персональных данных Пользователей.
9. ИСКЛЮЧИТЕЛЬНЫЕ ПРАВА НА КОНТЕНТ
9.1. Все объекты, размещенные на Сайте и в Программном продукте, в том числе элементы дизайна, текст, графические изображения, иллюстрации, видео, скрипты, программы, музыка, звуки и другие объекты и их подборки (далее — Контент), являются объектами исключительных прав Лицензиара, все права на эти объекты защищены.
9.2. Кроме случаев, установленных настоящим Соглашением, а также действующим законодательством Российской Федерации, Контент не может быть скопирован (воспроизведен), переработан, распространен, отображен во фрейме, опубликован, скачан, передан, продан или иным способом использован целиком или по частям без предварительного разрешения правообладателя, кроме случаев, когда правообладатель явным образом выразил свое согласие на свободное использование Контента любым лицом.
9.3. Использование Пользователем Контента, доступ к которому получен исключительно для личного некоммерческого использования, допускается при условии сохранения всех знаков авторства или других уведомлений об авторстве, сохранения имени автора в неизменном виде, сохранении произведения в неизменном виде.
9.4. Любое использование Контента, кроме разрешенного в настоящем Соглашении или в случае явно выраженного согласия правообладателя на такое использование, без предварительного письменного разрешения правообладателя, категорически запрещено.
10. ПРОЧИЕ УСЛОВИЯ
10.1. Все споры и разногласия, возникающие в связи с исполнением и (или) толкованием настоящего Соглашения, разрешаются Сторонами путем переговоров. При невозможности урегулирования Сторонами возникших разногласий путем переговоров, спор подлежит разрешению в арбитражном суде по месту нахождения ответчика с обязательным соблюдением претензионного порядка урегулирования споров и разногласий. Срок ответа на претензию 30 (тридцать) календарных дней с момента ее поступления в письменной форме или в электронном виде.
10.2. Ни одно из положений настоящего Соглашения не является и не может рассматриваться как передача (отчуждение) исключительных прав на интеллектуальную собственность Лицензиара.
10.3. В случае поступления от Пользователя замечаний к Программному продукту, предоставляемому в рамках настоящего Соглашения, такие замечания подлежат рассмотрению Лицензиаром по его желанию и необязательны для учета.
10.4. Условия настоящего Соглашения распространяются на последующие версии Программного продукта, которые являются его обновлениями. Заключения иных соглашений в отношении обновлений Программного продукта не требуется.
10.5. Во всем ином, что не предусмотрено настоящим Соглашением, Стороны руководствуются действующим законодательством РФ.
11. АДРЕС, РЕКВИЗИТЫ ЛИЦЕНЗИАРА
ООО «АЛЕКТА»
Юридический адрес: 630090, г. Новосибирск, Проспект академика Лаврентьева 2/2.
Почтовый адрес: 630090, г. Новосибирск, Проспект академика Лаврентьева 2/2.
ОГРН 1025403657135
ИНН 5408128408
КПП 540801001
ОКВЭД 72.19, 62.01, 62.02, 68.20.2;
ОКПО 26335100;
ОКАТО 50401384000;
ОКФС 16;
ОКОПФ 65.
E-mail: [email protected]
Молярная масса, расчет по формуле вещества
Молярная масса вещества складывает из суммы молярных масс атомов, входящих в химическую формулу. Атомные молярные массы — это константы, значения которых можно узнать в химическом справочнике (иногда атомные массы пишут прямо в периодической таблице элементов).
К примеру, молярная масса водорода (химическая формула молекулы водорода — H2) это удвоенная атомарная молярная масса элемента водород (H) :
1.0079 * 2 = 2.0158 г/моль
Для упрощения расчетов, особенно в школе, используют округленные значения молярных масс. Но компьютеру не сложно посчитать без округления, а также найти нужные молярные массы атомов в табличке за вас.
Калькулятор молярной массы
Все что нужно знать — это химическую формулу вещества.
Калькулятор распознаёт химические элементы в формуле и считает их общую массу. Но могут быть неоднозначности, к примеру формула h3CO3 (угольная кислота), написанная без учета регистра — h3co3 — будет воспринята калькулятором как h3Co3, т.е как некий гидрид Кобальта.
Чтобы помочь калькулятору распознать элементы в формуле, нужно учитывать регистр. Но на мобильном телефоне не удобно постоянно менять регистр ввода. В этом случае разделяйте хим. элементы пробелом. Увидев пробелы, программа сообразит, что это отдельные элементы.
Примеры формул, которые понимает калькулятор:
C8h20N4O2 (кофеин), (Nh5)2SO4 (сульфат аммония), 4Na2CO3 * 1.5 h3O2 (перкарбонат натрия), h3 s o 4 (серная кислота)
CaCO3 (Известняк, мел, мрамор)
Молярная масса 100.0872, г/моль
| # | Элемент | Масса, г/моль | N | Σ, г/моль |
|---|---|---|---|---|
| Ca | Кальций | 40.078 | 1 | 40.078 |
| C | Углерод | 12.011 | 1 | 12.011 |
| O | Кислород | 15.9994 | 3 | 47.9982 |
Уголок химика
Написать комментарийДанная запись опубликована в 21.12.2016 17:52 и размещена в На первой полосе. Вы можете перейти в конец страницы и оставить ваш комментарий.
Расчет веса стальной трубы по формуле
Довольно часто возникает потребность расчёта веса стального трубопроката, который собственно заключатся в расчёте веса одного погонного метра трубы.
В данной статье мы поможем сделать эти вычисления и узнать, вес трубы в зависимости от её характеристик.
Для расчёта веса трубы можно использовать несколько вариантов, одним из них является специальная таблица веса стальных труб, другим ГОСТ веса труб, а так же расчёт по специальным формулам.
Сегодня мы рассмотрим последний вариант, а именно расчёт веса трубы по формулам.
Данные формулы практически не отличаются по своим результатам, и вполне подходят для расчёта веса стального трубопроката.
Сразу стоит сказать, что имеющиеся две формулы расчёта массы трубы, не ограничиваются, какими то видами стальных труб, это могут быть и газовые и электросварочные трубы, расчёт их веса неизменен и результат будет верным (в пределах этих формул).
Зная формулы и необходимости расчёта веса стального металлопроката, в зависимости от его характеристик вы можете использовать одну из предложенных формул.
Теперь давайте перейдём непосредственно к формулам.
Первая формула по расчёту веса стального металлопроката:
Мп = ((Ду – Тс)/40,5)*Тс.
Где,
Ду – собственно диаметр стальной трубы, который измеряется в миллиметрах;
Тс – это толщина стенки стальной трубы, мера измерения миллиметры;
Мп – вес погонного метра трубы.
Теперь перейдём ко второй формуле расчёта веса труб из стали:
Вот собственно вторая наша формула: Мп = (Ду – Тс)*Тс*0,0246615,
Где,
Ду – диаметр стальной трубы, измеряемый в миллиметрах;
Тс – толщина стенки трубы из стали, единицы измерения миллиметры;
Мп – итоговый результат, как и в прошлой формуле, представляет собой вес одного погонного метра стальной трубы.
Как видите в данных формулах нет ничего сложного, для их использования и вычисления веса труб не требуется особых знаний и умений, достаточно знать формулы и иметь под ругой калькулятор.
Читайте так же:
Круг конструкционный
В чём разница между саморезами и шурупами
Характеристика процесса обогащения железных руд, виды обогащения руды
Что такое формула массы?
Масса — это свойство физических объектов и мера устойчивости этого тела к ускорению. Можно рассматривать массу объекта как меру того, сколько физического «вещества» составляет этот объект.
В отличие от реляционных свойств, таких как положение, скорость или потенциальная энергия, которые всегда должны определяться по отношению к другому объекту или контрольной точке, масса является внутренним свойством , которое объект имеет независимо от его отношения к другим вещам.Массу объекта можно рассчитать несколькими способами:
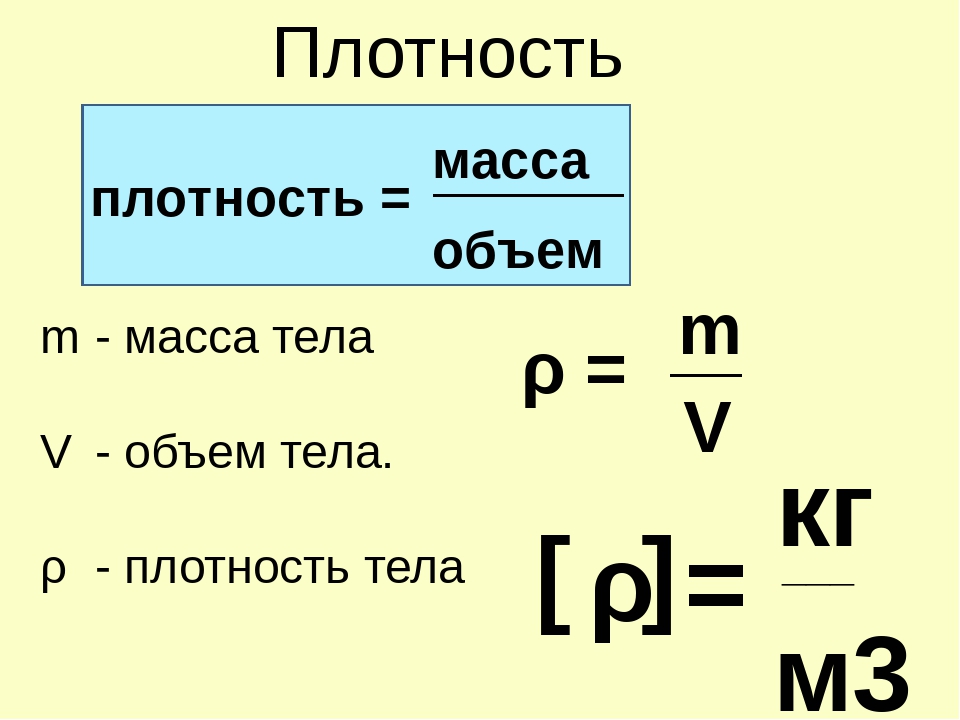
- масса = плотность × объем (m = ρV) . Плотность — это мера массы на единицу объема, поэтому массу объекта можно определить, умножив плотность на объем.
- масса = сила ÷ ускорение (м = F / a) . Согласно второму закону Ньютона (F = ma) ускорение объекта прямо пропорционально приложенной к нему силе. Следовательно, величина ускорения, сопровождающая приложение постоянной силы, обратно пропорциональна массе.
- масса = вес ÷ ускорение свободного падения (м = Вт / г). Вес — это произведение ускорения массы в гравитационном поле. В зависимости от силы ускорения свободного падения вес будет разным.
Все три формулы являются способом определения массы объекта. Поскольку масса является фундаментальным свойством, она не определяется в других единицах, как джоуль (Дж) ньютона (Н). Есть и другие способы вычисления массы объекта, но эти три формулы являются наиболее распространенными.
m = ρV
m = W / g
m = F / a
Единицы массы
Принятая в системе СИ единица измерения массы килограмм (кг). Килограмм — единственная основная единица СИ, имеющая в названии префикс (килограмм). Первоначально один килограмм определялся как масса одного кубического децилитра (дл) воды при температуре плавления. С 1889 года килограмм был переопределен как масса International Kilogram Prototype (IPK), физического артефакта, который должен был быть универсальной эталонной массой для килограмма.Первоначально ИПК представлял собой чугунную гирю. В настоящее время принятый ИПК представляет собой цилиндр высотой 39 мм из специального сплава платины.
«Слова тоже имеют подлинную сущность — массу, вес и удельный вес». — Тим О’Брайен
По состоянию на 2018 год килограмм — единственная единица СИ, в которой физический объект является опорным значением. Все остальные единицы СИ были переопределены с точки зрения фундаментальных физических констант, таких как скорость света или постоянная Планка.В ноябре 2018 года Генеральная конференция мер и весов (GCPM) проголосовала за переопределение килограмма с точки зрения фундаментальных физических констант, и это изменение вступит в силу 20 мая 2019 года.
Способы расчета массы
на основе плотности и объема
Плотность объекта, иногда обозначаемая греческой буквой «ρ», является мерой массы на единицу объема. По сути, плотность говорит вам, насколько плотно упакована масса объекта. Чем плотнее объект, тем больше у него массы на единицу объема.
Например, вода имеет плотность 977 кг / м 3 при стандартной температуре и давлении. То есть один кубометр воды имеет массу 977 кг. Если мы знаем плотность и объем вещества, мы также можем вычислить массу этого вещества. Допустим, у нас есть образец воды размером 0,7 м 3 . Какова масса этого образца?
Решение для массы дает:
m = ρV
m = (0,7 м 3 ) (977 кг / м 3 ) = 683 кг
0.5 кубометров воды при стандартной температуре и давлении имели бы массу 683 кг.
Некоторые объекты невероятно плотные. Например, нейтронная звезда имеет среднюю плотность 1,1 x 10 18 кг / м 3 . Одна чайная ложка нейтронной звезды на Земле будет весить около 100 миллионов тонн.
«Масса становится неподвижной; он не может маневрировать и, следовательно, не может одерживать победы, он может сокрушить только своим весом ». — Hans Von Seeckt
От силы и ускорения
Свойство массы также понимается как мера сопротивления физического объекта ускорению под действием внешней силы.Это понятие массы иногда называют инерционной массой . Инерция — это тенденция движущегося тела продолжать движение в постоянном состоянии, поэтому инерционная масса — это мера того, сколько инерции имеет тело и насколько сложно изменить его состояние движения. Связь между массой, силой и ускорением выражается вторым законом движения Ньютона F = ma. Это математическое соотношение говорит нам, что перед лицом постоянной силы более массивное тело будет ускоряться медленнее.Измеряя силу, приложенную к телу, и измеряя наблюдаемое ускорение, мы можем вычислить массу тела.
Например, предположим, что мы прикладываем силу 748 Н к металлическому кубу и измеряем его ускорение как 21 м / с 2 . Какая масса у металлического куба? Мы можем вычислить массу, разделив величину силы на величину ускорения:
м = F / a
м = (748 Н) / (21 м / с 2 ) ≈ 35,62 кг
Итак, мы знаем, что металлический куб должен иметь массу 35.62 кг.
From Вес
Строго говоря, вес и масса — разные вещи. В английском языке два слова «вес» и «масса» являются синонимами, но в физических науках они имеют разные значения. Масса — неизменное свойство, которое не меняется от места к месту. Вес — это мера силы гравитационного поля, действующего на массивное тело. Поскольку напряженность гравитационного поля может различаться, то есть Луна имеет более слабую напряженность гравитационного поля, чем Земля, вес объекта может различаться в разных средах.
Связь между массой и весом определяется выражением W = mg, где g — мера ускорения свободного падения. Точное значение g различается в зависимости от местоположения. На Земле g имеет значение приблизительно 9,81 м / с 2 , а на Луне g составляет около 1,6 м / с 2 . Выражение W = мг дает вес в ньютонах, в то время как повседневное понимание веса дано в фунтах (фунтах), коэффициент преобразования из ньютонов в фунты составляет около 1 Н = 0,22 фунта.
Например, на поверхности Земли где g = 9.81 м / с 2 , объект весом 50 кг будет иметь вес в фунтах:
W = (50 кг) (9,81 м / с 2 ) = 490,5N
Преобразование ньютонов в фунты дает:
490,5 Н (0,22 фунта / 1 Н) ≈ 108 фунтов
И наоборот, на Луне, где g имеет значение 1,6 м / с 2 , объект весом 50 кг будет весить:
W = 50 (кг) ( 1,6 м / с 2 ) (0,22 фунта / 1 Н) ≈ 18 фунтов
Тот же объект весом 50 кг весит 108 фунтов на Земле и 18 фунтов на Луне.
Точно так же, если мы знаем вес объекта, мы можем работать в обратном направлении, чтобы вычислить его массу. Скажем, объект весит 160 фунтов Земли. мы можем рассчитать массу объекта как:
180 фунтов (1N / 0,22 фунта) = 818,18N
818,18N = м (9,81 м / с 2 )
м = 818,18N / (9,81 м / с 2 ) ≈ 83,4 кг
Итак, тело весом 180 фунтов на Земле имеет массу около 84,3 кг.
Эквивалентность массы и энергии
В течение очень долгого времени ученые считали, что массу объекта можно считать полностью независимой от других его свойств.Однако в начале 20 века специальная теория относительности Эйнштейна показала, что масса и энергия на самом деле являются двумя разными названиями одной и той же физической величины. В частности, масса объекта и его полная энергия связаны знаменитым уравнением Эйнштейна E = mc 2 , где c — скорость света в вакууме.
E = mc 2 говорит нам, что полная энергия неподвижного тела прямо пропорциональна его массе с коэффициентом c 2 . Поскольку c = 3 000 000 м / с, c 2 является чрезвычайно большим фактором.Следовательно, даже крошечный кусочек массы содержит огромное количество внутренней энергии. Чтобы рассмотреть вопрос в перспективе, общее количество энергии от полного преобразования 1 грамма вещества в энергию примерно равно 21,5 килотоннам в тротиловом эквиваленте — силе атомной бомбы в Хиросиме.
«Любой дурак может знать. Дело в том, чтобы понять ». — Альберт Эйнштейн
В определенных физических процессах, таких как ядерное деление или движение тела в сильном гравитационном поле, материя преобразуется в энергию и выделяется в виде большого количества света и тепла.В частности, уравнение Эйнштейна говорит нам, как мы можем рассчитать количество энергии, выделяющейся во время таких реакций.
Скажем, 30 кг урана (Ur) загружают в ядерный реактор. Во время деления примерно 0,1% этой массы полностью превращается в энергию. Сколько энергии получается?
0,1% от 30 кг составляет 0,3 кг. Подставив это в уравнение Эйнштейна, мы получим:
E = (0,3 кг) (3,000,000) 2 = (0,3) (8,98755179 × 10 16 ) = 2,69626554 × 10 16 J
Полное преобразование всего 0 .3 кг (0,6 фунта) вещества превращаются в энергию, выделяя 2,69626554 × 10 16 Дж энергии. Это примерно столько же, сколько взорвано более 6 миллионов тонн тротила (12 миллиардов фунтов), чего достаточно, чтобы полностью сравнять с землей даже самые большие города.
Мы также можем работать в обратном направлении от некоторого количества энергии, чтобы определить количество преобразованной массы. Скажем, некоторая реакция деления высвобождает 1,6178 × 10 16 джоулей энергии. Сколько массы было преобразовано в энергию во время этого процесса? Используя нашу удобную формулу эквивалентности массы и энергии, мы можем определить:
1.6178 × 10 16 J = м (8,98755179 × 10 16 )
(1,6178 × 10 16 ) / 8,98755179 × 10 16 ) = м
м ≈ 0,18 кг
Таким образом, примерно 0,18 кг масса была преобразована в энергию.
Почему объекты имеют массу?
Только недавно ученые начали открывать ответ на вопрос, почему частицы вообще имеют массу. В 1960-х годах несколько ученых заметили некоторые проблемы со своими уравнениями, описывающими поведение элементарных частиц.В частности, их уравнения предсказывали, что определенные частицы, генерируемые во время высокоскоростных столкновений, не будут иметь массы. Однако экспериментальное наблюдение показало, что эти частицы действительно имели ненулевую массу.
Ученые предположили, что масса бозона может быть образована взаимодействием между этими бозонами и всепроникающим полем, называемым полем Хиггса (в честь одного из его теоретиков Питера Хиггса). Когда безмассовые бозоны движутся против этого поля, их импульс замедляется, и они теряют некоторую энергию.Поле Хиггса преобразует эту энергию в массу-энергию, которая проявляется как масса свойства, которую мы измеряем. Было предсказано, что это взаимодействие между бозонами и полем Хиггса приведет к созданию новой частицы, крошечного бозона, получившего название бозона Хиггса. Ускоритель элементарных частиц в ЦЕРНе наконец продемонстрировал существование частицы Хиггса в 2013 году, а 8 октября 2013 года Питер Хиггс и Франсуа Энглерт были удостоены Нобелевской премии по физике за их теоретические работы по частице.
Была ли эта статья полезной?
😊 ☹️ Приятно слышать! Хотите больше научных тенденций? Подпишитесь на нашу рассылку новостей науки! Нам очень жаль это слышать! Мы любим отзывы 🙂 и хотим, чтобы вы внесли свой вклад в то, как сделать Science Trends еще лучше.Калькулятор массы
Это основной калькулятор массы, основанный на плотности и объеме. Этот калькулятор берет и генерирует результаты многих распространенных единиц измерения.
Что такое масса?
Масса обычно определяется как количество вещества внутри объекта. Чаще всего она измеряется как инерционная масса, включающая сопротивление объекта ускорению с учетом некоторой чистой силы. Однако материя в науке определяется нечетко и не может быть точно измерена. В классической физике материя — это любое вещество, имеющее массу и объем.
Количество массы объекта часто коррелирует с его размером, но объекты с большим объемом не всегда имеют большую массу. Например, надутый шар имел бы значительно меньшую массу, чем мяч для гольфа, сделанный из серебра. Хотя во всем мире для описания массы используется множество различных единиц, стандартной единицей массы в Международной системе единиц (СИ) является килограмм (кг).
Существуют и другие общие определения массы, включая активную гравитационную массу и пассивную гравитационную массу.Активная гравитационная масса — это мера того, сколько гравитационной силы проявляет объект, в то время как пассивная гравитационная масса — это мера гравитационной силы, действующей на объект в пределах известного гравитационного поля. Хотя они концептуально различны, не было проведено убедительных однозначных экспериментов, которые продемонстрировали бы существенные различия между гравитационной и инертной массой.
Зависимость массы от массы
Слова масса и вес часто используются как синонимы, но даже несмотря на то, что масса часто выражается путем измерения веса объекта с помощью пружинных весов, они не эквивалентны.Масса объекта остается постоянной независимо от того, где находится объект, и поэтому является внутренним свойством объекта. С другой стороны, вес изменяется в зависимости от силы тяжести, поскольку он является мерой сопротивления объекта его естественному состоянию свободного падения. Например, сила тяжести на Луне составляет примерно одну шестую, чем на Земле, из-за ее меньшей массы. Это означает, что человек с массой 70 кг на Земле будет весить примерно одну шестую своего веса на Земле, находясь на Луне.Однако их масса на Луне по-прежнему будет составлять 70 кг. Это соответствует уравнению:
В приведенном выше уравнении F — сила, G — гравитационная постоянная, m 1 и m 2 — масса Луны и объекта, на который она действует, а r — радиус луны. В обстоятельствах, когда гравитационное поле постоянно, вес объекта пропорционален его массе, и нет проблем с использованием одних и тех же единиц для выражения обоих.
В метрической системе вес измеряется в Ньютонах по уравнению W = мг , где W — вес, м — масса и г — ускорение, вызванное гравитационным полем. На Земле это значение составляет примерно 9,8 м / с 2 . Важно отметить, что независимо от того, насколько сильным может быть гравитационное поле, объект, который находится в свободном падении, невесом. В случаях, когда объекты подвергаются ускорению за счет других сил (например, центрифуги), вес определяется путем умножения массы объекта на общее ускорение от свободного падения (известное как собственное ускорение).
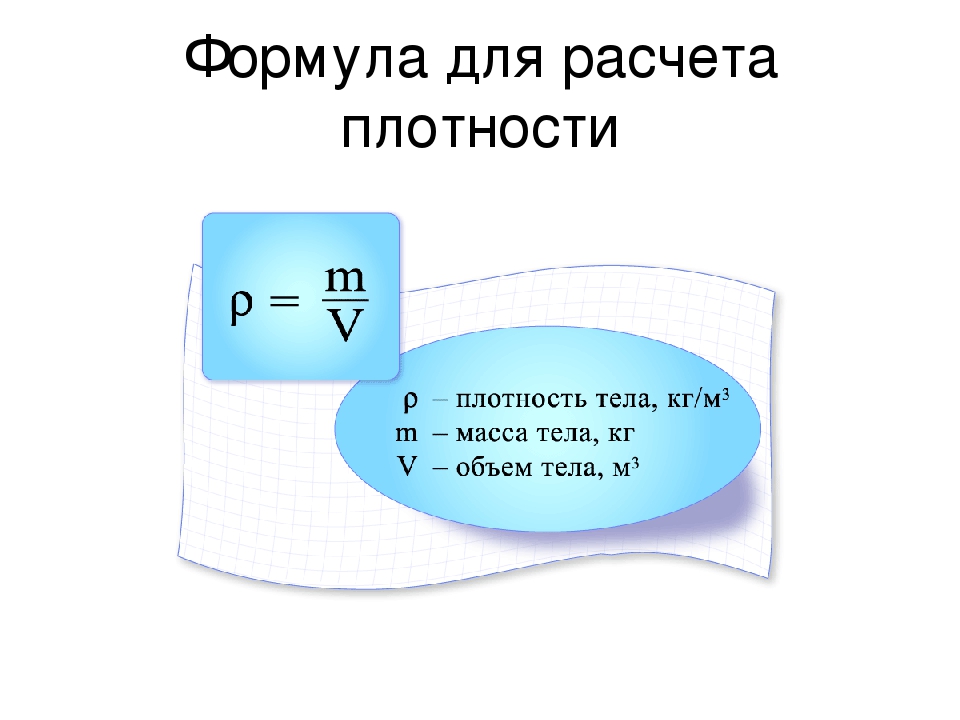
Хотя масса определяется как F = ma, в ситуациях, когда известны плотность и объем объекта, масса также обычно вычисляется с использованием следующего уравнения, как в калькуляторе:
м = ρ × V
В приведенном выше уравнении м, — масса, ρ — плотность и V — объем. Единица измерения плотности в системе СИ — килограмм на кубический метр, или кг / м 3 , объем выражается в м 3 , а масса — в кг .Это перестановка уравнения плотности. Более подробная информация доступна на калькуляторе плотности.
Формула массы: определение и примеры — видео и стенограмма урока
Расчет и измерение массы
Есть два способа определить массу объекта. Первый метод включает в себя немного математики. Масса вводится в физику , Второй закон движения Ньютона . В этом законе Ньютон утверждает, что когда вы складываете все силы, действующие на объект, называемые суммой сил или чистой силой, и эта сумма не равна нулю, тогда этот объект ускоряется.Этот закон гласит, что сила, действующая на объект, пропорциональна ускорению, которое испытывает объект. Это означает, что если сила увеличивается, ускорение увеличивается, и наоборот, если сила уменьшается, то ускорение уменьшается. Константа пропорциональности силы и ускорения называется массой. Более конкретно, это называется инертной массой.
Инерционная масса определяется как сопротивление объекта ускорению. Это означает, что чем больше инерционная масса, тем труднее ускорить этот объект.Давайте снова посмотрим на наши шары для боулинга и пинг-понга. Если я приложу одинаковую силу к обоим шарикам, какой объект будет иметь большее ускорение? Ответ — шар для пинг-понга, потому что он имеет меньшую инерционную массу и, следовательно, его будет легче ускорить, чем шар для пинг-понга, чем шар для боулинга. Эта система уравнений дает нам формулу для расчета массы объекта, если мы знаем силу, действующую на него, и ускорение объекта:
Чистая сила объекта равна массе, умноженной на ускорение.Массу можно рассчитать, разделив чистую силу, действующую на объект, на его ускорение. Говоря о чистой силе, мы используем единицы килограмм-метр на секунду в квадрате. Это также известно как Ньютон. Единицы измерения ускорения — квадратные метры в секунду, а единицы массы — килограммы.
Давайте сделаем пример. Вы толкаете тележку на 8,0 Ньютона, заставляя ее ускоряться со скоростью 0,50 м / с / с.Какая масса у корзины покупок?
Мы знаем, что масса равна чистой силе, деленной на ускорение. Мы знаем, что чистая сила равна 8 Ньютонам, или 8 килограммам на секунду в квадрате. Ускорение составляет 0,5 метра в секунду в квадрате. Метры на секунду в квадрате компенсируют друг друга, и затем мы делим 8 на 0,5, что означает, что мы получаем массу в 16 килограммов. Как видите, если вы знаете силу, действующую на объект, и ускорение, возникающее в результате этой силы, вы сможете рассчитать массу объекта.
Для большинства объектов вам не нужно знать силу или ускорение, если у вас есть масштаб. Второй метод, используемый для определения массы объекта, — это просто поставить объект на весы. Если на весах указаны граммы или килограммы, это измерение массы. Любая шкала с фунтами измеряет вес, который, как мы теперь знаем, представляет собой совершенно другое измерение. Конечно, для некоторых объектов, таких как корабль или автомобиль, очень сложно найти масштаб для таких массивных объектов.Затем в этих случаях вы можете разрабатывать эксперименты, в которых вы прикладываете к объекту известную силу, а затем измеряете результирующее ускорение. Затем вы можете определить массу большого объекта.
Резюме урока
Масса — это мера того, сколько материала находится в объекте. Более формально масса или инерционная масса — это мера сопротивления ускорению. Чем больше инерционная масса, тем труднее разогнать объект. Мы можем либо измерить массу с помощью шкалы, либо вычислить массу объекта.Однако, чтобы рассчитать массу объекта, нам нужно знать силу, действующую на объект, и результирующее ускорение.
Как рассчитать массу и вес
Обновлено 1 февраля 2020 г.
Кевин Бек
Рецензент: Lana Bandoim, B.S.
Если вы проводите какое-то время, общаясь с людьми на работе или в школе, и смотрите какие-либо телепрограммы, для вас было бы необычно провести даже целый день, не услышав хотя бы одно из слов масса или вес.Это особенно верно в отношении последнего, учитывая количество людей, которые в любое время пытаются похудеть с помощью некоторой комбинации физической активности и модификации диеты.
Определение массы и веса объектов в современном мире достаточно просто: найдите весы подходящего размера, поместите на них объект и прочитайте полученные цифровые или аналоговые числа. Но вычисление массы по весу или наоборот может сбивать с толку, потому что эти термины используются неправильно или неточно в повседневном языке.
Что такое масса в физике?
Масса — одна из двух фундаментальных величин в физике, вторая — длина. Под «фундаментальным» это означает, что все другие единицы (например, скорость, сила, ускорение и т. Д.) Являются производными от одной или нескольких из этих единиц, тогда как ни масса, ни длина сами по себе не выводятся.
Масса — это мера «вещества», не считая того влияния, которое на него оказывает гравитация. На корневом уровне все, что имеет массу, состоит из электронов, протонов и нейтронов (или, если хотите, субатомных частиц).Одним из ключевых свойств массы является то, что гравитация действительно действует на нее, если она присутствует, в результате чего возникает сила, называемая вес .
- Для справки, 1 кг = 2,204 фунта, считая фунт в «повседневном» земном смысле.
Что такое вес в физике?
Вес является результатом действия силы тяжести на массу: w = мг. Значение g на поверхности Земли составляет 9,8 м / с 3 с единицей ускорения . Чтобы найти вес чего-либо, просто умножьте его массу на значение местного гравитационного поля, и вы получите результат в ньютонах (N).Например, если ваша масса составляет 50 кг (около 110 фунтов), то ваш вес равен (50) (9,8).
Следует особо подчеркнуть то, что вес — это сила. Масса не требует гравитации для своего существования, в отличие от веса. Их легко объединить, потому что кто-либо на Земле редко работает в условиях невесомости.
По этой причине, когда вы рассчитываете свою массу на весах, предназначенных для использования на Земле, вес уже учитывается при работе весов.Масса не есть вес, но они всегда прямо пропорциональны друг другу величиной g, какой бы она ни была.
Но что это означает в имперских единицах (фунтах и унциях)? Фактически, в этой схеме существует единица массы, называемая снарядом, но сегодня она игнорируется. Если кто-то говорит, что она весит 110 фунтов, считайте это ее массой, которая составляет 50 кг в единицах СИ.
Расчет массы на основе других переменных
Масса и длина вместе дают начало важной переменной, называемой плотностью.Объем, который является мерой «куска» трехмерного пространства, выводится из единиц длины, а в метрической системе он имеет единицы измерения m 3 . Плотность — это масса, разделенная на объем, и дает представление о «тяжести» объекта по отношению к его размеру.
В числовом выражении плотность ρ = м / В и имеет единицы СИ: кг / м 3 , хотя такие единицы, как г / см 3 , более распространены в научных учреждениях.
- Какова масса объекта размером 0,25 м 3 с плотностью 2.5 кг / м 3 ?
Поскольку ρ = m / V, m = ρV. В данном случае:
(0,25 м3) (2,5 кг / м 3 ) = 0,625 кг.
Вычислить массу на основе задачи примера плотности
Плотность — это количество вещества или массы на единицу объема. В этом примере задачи показано, как вычислить массу объекта по известной плотности и объему.
Простой пример (метрические единицы)
В качестве примера простой задачи найдите массу куска металла объемом 1.25 м 3 и плотностью 3,2 кг / м 3 .
Во-первых, вы должны заметить, что и объем, и плотность используют объем в кубических метрах. Это упрощает расчет. Если бы эти две единицы не были одинаковыми, вам нужно было бы преобразовать одну, чтобы они соответствовали друг другу.
Затем измените формулу плотности, чтобы найти массу.
Плотность = Масса ÷ Объем
Умножьте обе части уравнения на объем, чтобы получить:
Плотность x Объем = Масса
или же
Масса = Плотность x Объем
Теперь вставьте числа, чтобы решить проблему:
Масса = 3.2 кг / м 3 x 1,25 м 3
Если вы видите, что единицы не отменяются, значит, вы сделали что-то не так. Если это произойдет, измените условия, пока проблема не исчезнет. В этом примере кубические метры сокращаются, оставляя килограммы, которые являются единицей массы.
Масса = 4 кг
Простой пример (английские единицы)
Найдите массу капли воды объемом 3 галлона. Это кажется достаточно простым. Большинство людей запоминают плотность воды как 1.Но это в граммах на кубический сантиметр. К счастью, легко узнать плотность воды в любой единице.
Плотность воды = 8,34 фунта / галлон
Итак, проблема становится:
Масса = 8,34 фунта / галлон x 3 галлона
Масса = 25 фунтов
Проблема
Плотность золота 19,3 грамма на кубический сантиметр. Какова масса слитка золота в килограммах размером 6 дюймов на 4 дюйма на 2 дюйма?
Решение
Плотность равна массе, деленной на объем.
D = m / V
, где
D = плотность
m = масса
V = объем
У нас есть плотность и достаточно информации, чтобы найти объем в задаче. Остается только найти массу. Умножьте обе части этого уравнения на объем V и получите:
m = DV
Теперь нам нужно найти объем золотого слитка. Плотность, которую нам дали, выражается в граммах на кубический сантиметр, а полоса измеряется в дюймах. Во-первых, мы должны преобразовать дюймовые измерения в сантиметры.
Используйте коэффициент преобразования 1 дюйм = 2.54 сантиметра.
6 дюймов = 6 дюймов x 2,54 см / 1 дюйм = 15,24 см.
4 дюйма = 4 дюйма x 2,54 см / 1 дюйм = 10,16 см.
2 дюйма = 2 дюйма x 2,54 см / 1 дюйм = 5,08 см.
Умножьте все эти три числа вместе, чтобы получить объем золотого слитка.
V = 15,24 см x 10,16 см x 5,08 см
V = 786,58 см 3
Поместите это в формулу выше:
м = DV
м = 19,3 г / см 3 x 786,58 см 3
м = 14833,59 грамма
Ответ, который нам нужен, — это масса золотого слитка в килограммах.В 1 килограмме 1000 грамм, поэтому:
масса в кг = масса в г x 1 кг / 1000 г масса
в кг = 14833,59 г x 1 кг / 1000 г масса
в кг = 14,83 кг.
Ответ
Масса золотого слитка в килограммах размером 6 дюймов на 4 дюйма на 2 дюйма составляет 14,83 кг.
Советы для успеха
- Самая большая проблема, с которой сталкиваются учащиеся, решая массу, — это неправильная постановка уравнения. Помните, масса равна плотности, умноженной на объем.Таким образом, единицы объема уравновешиваются, оставляя единицы массы.
- Убедитесь, что единицы измерения объема и плотности работают вместе. В этом примере смешанные метрические и английские единицы были намеренно использованы, чтобы показать, как конвертировать единицы.
- Единицы измерения объема, в частности, могут быть непростыми. Помните, что при определении объема необходимо применять правильную формулу.
Сводка формул плотности
Помните, что вы можете составить одну формулу для вычисления массы, плотности или объема.Вот три уравнения, которые можно использовать:
- Масса = Плотность x Объем
- Плотность = Масса ÷ Объем
- Объем = Масса ÷ Плотность
Узнать больше
Для получения дополнительных примеров задач используйте Рабочие задачи химии. Он содержит более 100 различных рабочих примеров задач, полезных для студентов-химиков.
Источник
- «Справочник таблиц CRC для прикладных инженерных наук», 2-е издание.CRC Press, 1976, Бока-Ратон, Флорида,
Формула массы: определение и пример расчета
Масса по формуле молекулы (также известная как масса по формуле ) — это сумма атомных масс атомов в эмпирической формуле соединения. Формула веса дается в атомных единицах массы (а.е.м.).
Пример и расчет
Молекулярная формула глюкозы: C 6 H 12 O 6 , поэтому эмпирическая формула CH 2 O.
Формула массы глюкозы составляет 12 + 2 (1) +16 = 30 а.е.м.
Определение относительной формулы массы
Вы должны знать родственный термин — относительная масса по формуле (относительный вес по формуле). Это просто означает, что расчет выполняется с использованием значений относительной атомной массы элементов, которые основаны на естественном изотопном соотношении элементов, обнаруженных в атмосфере и коре Земли. Поскольку относительный атомный вес является безразмерным значением, относительная масса по формуле технически не имеет каких-либо единиц.Однако часто используются граммы. Если относительная формульная масса дана в граммах, то она рассчитана на 1 моль вещества. Обозначение относительной формулы массы — M r , и она рассчитывается путем сложения значений A r всех атомов в формуле соединения.
Расчет относительной массы по формуле
Найдите относительную формулу массы оксида углерода, CO.
Относительная атомная масса углерода равна 12, а кислорода — 16, поэтому относительная масса по формуле:
12 + 16 = 28
Чтобы найти относительную формульную массу оксида натрия, Na 2 O, вы умножаете относительную атомную массу натрия на ее нижний индекс и прибавляете полученное значение к относительной атомной массе кислорода:
(23 х 2) + 16 = 62
Один моль оксида натрия имеет относительную формульную массу 62 грамма.
Грамм Формула Масса
Масса по формуле в граммах — это количество соединения с такой же массой в граммах, что и масса по формуле в а.е.м. Это сумма атомных масс всех атомов в формуле, независимо от того, является ли соединение молекулярным. Масса по формуле грамма рассчитывается как:
грамм формула масса = масса растворенного вещества / формула масса растворенного вещества
Обычно вас просят указать массу по формуле в граммах на 1 моль вещества.
Пример
Найти по формуле грамма масса 1 моля KAl (SO 4 ) 2 · 12H 2 O.
Помните, умножьте значения атомных единиц массы атомов на их индексы. Коэффициенты умножаются на все последующее. В данном примере это означает, что имеется 2 сульфат-аниона согласно нижнему индексу и 12 молекул воды согласно коэффициенту.
1 K = 39
1 Al = 27
2 (SO 4 ) = 2 (32 + [16 x 4]) = 192
12 H 2 O = 12 (2 + 16) = 216
Итак, масса по формуле грамма составляет 474 г.
Источник
- Paul, Hiemenz C.; Тимоти, Лодж П. (2007). Химия полимеров (2-е изд.). Бока-Ратон: CRC P, 2007. 336, 338–339.
Массово-мольные вычисления Учебное пособие по химии
Ключевые понятия
- 1 моль чистого вещества имеет массу, равную его молекулярной массе (1) , выраженной в граммах.
Она известна как молярная масса M и измеряется в г моль -1 (граммы на моль вещества).
- Взаимосвязь между молярной массой, массой и молями может быть выражена математическим уравнением, как показано ниже:
г моль -1 = г ÷ моль
молярная масса = масса ÷ моль
M = m ÷ n
где:
M = молярная масса чистого вещества (измеряется в г · моль -1 )
m = масса чистого вещества (измеряется в граммах, г)
n = количество чистого вещества (измеряется в молях, моль) - Это математическое уравнение можно преобразовать в следующее:
п = м ÷ М
моль = масса ÷ молярная массам = n × M
масса = моль × молярная масса - Для расчета молей чистого вещества: n = m ÷ M
- Для расчета массы чистого вещества: m = n × M
- Для расчета молярной массы чистого вещества: M = m ÷ n
Пожалуйста, не блокируйте рекламу на этом сайте.
Без рекламы = для нас нет денег = для вас нет бесплатных вещей!
Расчет массы чистого вещества (m = нМ)
1 моль чистого вещества определяется как имеющий массу в граммах, равную его относительной молекулярной массе.
Эта величина известна как молярная масса (символ M).
Итак, масса 1 моля чистого вещества = относительная молекулярная масса в граммах.
А, масса 1 моля чистого вещества = молярная масса чистого вещества (г моль -1 )
Или, масса 1 моля = M (г моль -1 )
В таблице ниже указана масса 1 моля ряда обычных чистых веществ:
| название | молекулярная формула | относительная молекулярная масса | молярная масса (г моль -1 ) | масса 1 моль (г) |
|---|---|---|---|---|
| газообразный гелий | He | 4.003 | 4,003 г моль -1 | 4,003 г |
| газообразный кислород | O 2 | 2 × 16,00 = 32,00 | 32,00 г моль -1 | 32308 |
| CO 2 | 12,01 + (2 × 16,00) = 44,01 | 44,01 г моль -1 | 44,01 г | |
| жидкая вода | H 2 O | (2 × 1,008) + 16.00 = 18,016 | 18,016 г моль -1 | 18,016 г |
Из таблицы видно, что 1 моль воды имеет массу 18,016 грамма, что не очень много (примерно по массе воды в паре маленьких кубиков льда, которые вы бы сделали в своей семейной морозильной камере).
А что, если бы у вас было 10 молей воды? Какой будет масса 10 молей воды?
Если 1 моль воды имеет массу 18,016 г, то 10 моль воды должны иметь массу в десять раз больше:
масса 10 моль воды = 10 × масса 1 моля воды
масса 10 моль воды = 10 × 18.016 = 180,16 г (примерно масса воды, которую можно налить в небольшой стакан)
Итак, если бы у нас было только ½ моля воды, какая масса воды была бы у нас?
Если 1 моль воды имеет массу 18,016 г, то ½ моля воды должно иметь ½ массы:
масса ½ моля воды = ½ × масса 1 моля воды
масса ½ моля воды = ½ × 18,016 = 9,008 г
В обоих приведенных выше примерах мы можем вычислить массу воды в граммах, умножив количество молей воды на массу 1 моля воды в граммах:
масса воды = моль воды × масса 1 моля воды
, поскольку масса 1 моля воды в граммах известна как его молярная масса, мы можем записать:
масса воды = моль воды × молярная масса воды
В таблице ниже сравнивается масса различных количеств воды в молях, и данные представлены в виде графика справа:
| |||||||||||||||||||||||||||||
| Из данных в таблице мы можем обобщить и сказать, что для любого чистого вещества масса вещества в граммах равна молям вещества, умноженным на массу 1 моля вещества: масса = моль × масса 1 моля и поскольку масса 1 моля вещества (в граммах) = молярная масса (в граммах на моль) масса (г) = моль × молярная масса (г моль -1 ) м = n × M | На приведенном выше графике показана прямая линия, проходящая через начало координат (0,0), поэтому уравнение для прямой выглядит следующим образом: y = наклон × x где y — масса воды (г) и x — моль воды (моль) и наклон (уклон) линии = вертикальный подъем ÷ горизонтальный ход = 270.24 г ÷ 15 моль = 18,016 г моль -1 = молярная масса воды (г моль -1 ) Итак, уравнение для этой линии: масса (H 2 O) = молярная масса (H 2 O) × моль (H 2 O) В целом: масса (г) = молярная масса (г-моль -1 ) × моль (моль) |
Выполните следующие действия, чтобы рассчитать массу чистого вещества с учетом количества вещества в молях:
- Извлеките данные из вопроса:
масса = m =? (единицы — граммы)
родинок = n = запишите, что вам сказали в вопросе
молярная масса = M = запишите, что вам сказали в вопросе (единицы измерения: г моль -1 )
(вам может потребоваться вычислить это, используя молекулярную формулу чистого вещества и Периодическую таблицу) - Проверить единицы на соответствие и при необходимости преобразовать:
Количество вещества должно быть в молях (моль)!
Если количество указано в миллимолях (ммоль), разделите его на 1000, чтобы получить количество в молях (моль).
Если количество указано в микромолях (мкмоль), разделите его на 1 000 000, чтобы получить количество в молях (моль).
Если количество указано в километрах (кмоль), умножьте его на 1000, чтобы получить количество в молях (моль). - Напишите математическое уравнение (математическую формулу):
масса = моль × молярная масса
или
м = n × M - Подставьте значения и решите уравнение, чтобы найти значение массы m в граммах (г).
Расчет молей чистого вещества (n = m / M)
В приведенном выше обсуждении мы обнаружили, что можем рассчитать массу чистого вещества, используя моль и молярную массу вещества:
масса (г) = моль (моль) × молярная масса (г-моль -1 )
Как бы мы вычислили количество молей чистого вещества, если бы мы знали массу вещества?
(a) Мы могли бы использовать некоторую алгебру: разделите обе части уравнения на молярную массу:
| масса | = | моль × | ||||||||||||||||||||||||||||
| молярная масса | молярная масса моль = масса ÷ молярная масса п = м ÷ М (b) Мы могли бы использовать некоторую логику:
При рассмотрении единиц мы видим, что деление молярной массы на массу даст нам количество в единицах «моль -1 ». молярная масса / масса = Если мы перевернем это вверх дном (в математических терминах, возьмем обратную величину), мы получим количество в единицах «моль», которое нам и нужно: масса / молярная масса = так моль = масса ÷ молярная масса п = м ÷ М Выполните следующие действия, чтобы рассчитать количество чистого вещества в молях с учетом массы вещества:
Расчет молярной массы чистого вещества (M = m / n) Что, если бы вы знали количество чистого вещества в молях и его массу? Напомним, что масса = моль × молярная масса или m = n × M (a) Мы могли бы использовать некоторую алгебру: разделите обе части уравнения на моли:
|
